Why probability is necessary?
확률적 표현이 필요한 이유?
1. 확률 몰라도 되던데
우리는 보통 일상생활에서 측정된 정보를 주어진 그대로 믿는 경우가 많습니다. 방의 사이즈에 맞는 가구를 주문하기 위해 방의 가로 세로 크기를 재보기도하고, 운전 중 과속으로 딱지를 떼지 않기 위해 계기판에 찍혀 있는 자신의 주행 속도를 확인하기도 하고, 몸무게를 재서 다이어트를 시작하기도 하죠…
사실 academic 하게든, 아니면 실무적으로 센서 신호를 처리하는 일을 해본 적 이 없다면 확률에 대해서 그렇게 까지 깊게 고민해 본적이 없을 겁니다. 아니, 깊게 고민하지 않아도 사는데 전혀 지장이 없습니다. 아무도 자신의 측정된 몸무게의 평균값과 표준 편차를 필요로 하지 않으니까요. ㅎ
2. 확률을 생각안했더니
그럼에도 불구하고, 확률적 표현이 필요한 순간이 옵니다. 앞에서 든 예시처럼 측정된 정보를 그대로 받아들이면 끝! 인 경우는 그렇다 쳐도, 센서에서 나온 값을 가지고 더 의미있는 정보를 뽑아내고 싶은 경우가 그렇습니다. 그런 경우가 어떤게 있냐구요? 가속도와 각속도를 측정할 수 있는 센서인 IMU를 예시로 들어보겠습니다.
만약 IMU를 들고 움직이면서 자신이 움직인 거리 정보를 계산하고 싶다면 어떻게 해야할까요? 제일 먼저 할 수 있는 기본적인 생각은, 가속도를 두 번 적분하고, 각속도를 한 번 적분해서 자신의 위치를 실시간으로 파악하는 것일 겁니다. 하지만 만약에 내가 산 IMU가 엄청 싼 저가형 IMU라서 노이즈가 심하다고 해봅시다. 즉, 가만히 서있으면 가속도가 0이 나와야 하지만 $\pm0.1m/s^2$ 사이의 값이 무작위하게 히는 상태입니다.
저 정도 작은 값이 그래도 무슨 상관이냐구요? 그렇다면 이렇게 생각해볼까요? 1초에 한 번씩 위치를 계산한다고 하면 가속도 값이 $0.1m/s^2$ 일 때 이동한 위치 값은 0.1m 가 됩니다. 다음 계산 순간에 가속도 값이 고맙게도 $-0.1m/s^2$ 가 찍힌다면 우리는 다시 위치가 0m 가 되어서 움직이지 않는 상태를 잘 표현할 수 있겠지만, 앞서 표현한대로 센서의 값은 일정 범위 내에서 무작위하게 나오고 있습니다. 불과 2초 동안의 위치도 이렇게 불안정한데, 이런 계산을 1시간정도 하면 어떨까요? 아니면 애초에 센서에 바이어스가 있다면 어떨까요? 결국에는 전혀 엉뚱한 위치값을 계산하게 될 것입니다.
3. 그럼 확률 아는사람은
위와 같은 문제로 캡스톤 디자인을 실패할 것 같은 예감이 들어 절망하고 있는 학부생을 지나가는 대학원생이 보았습니다. 그 대학원생은 자기 졸업논문이 바쁨에도 불구하고, IMU의 신호가 출력되는 확률적인 분포와, 신호가 출력되지 않는 동안 물체가 어떤 움직임을 가질 지에 대한 확률적인 고려를 통하여 멋들어지게 학부생을 구해줬습니다. 그리고 귀에다가 속삭입니다. “칼만필터… 아세요?”
결론을 말하기 위해 상당히 긴 빌드업을 했는데, 결국 측정된 신호 값을 그대로 쓰면 나오게 되는 각종 문제들을 해결하기 위해서 우리는 확률을 알아야 하며, 확률 기반 모델링은 신호처리의 근간이 된다고 말할 수 있겠습니다. 긴글 읽어주셔서 감사합니다!
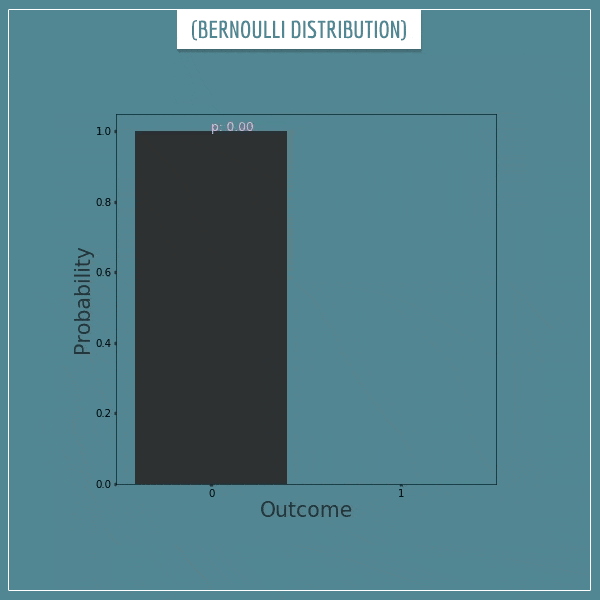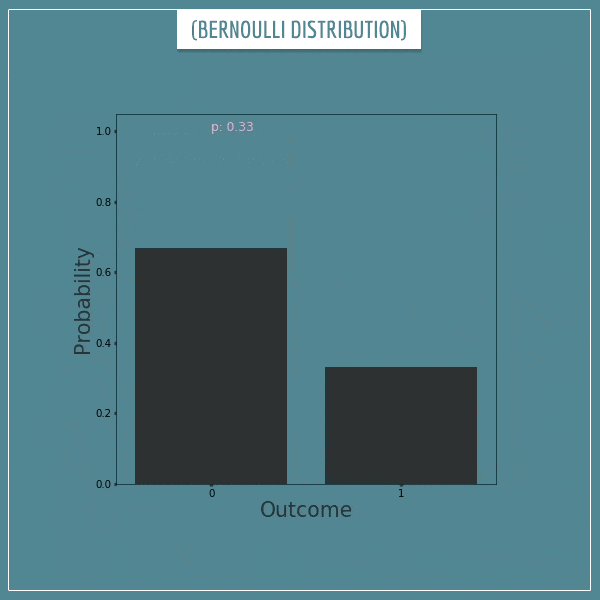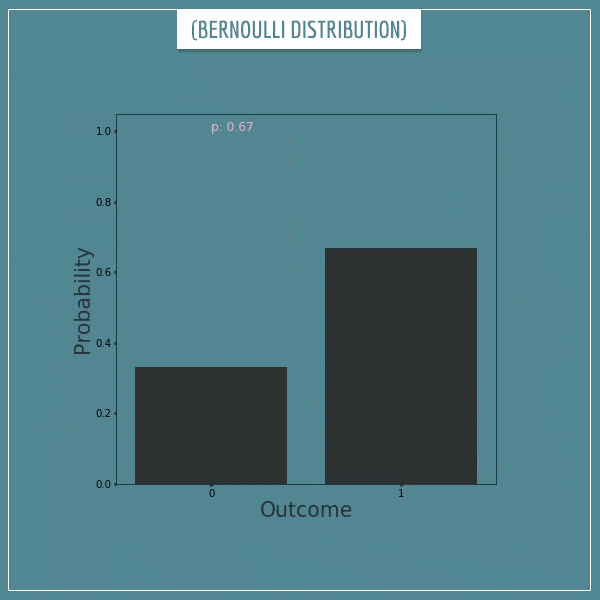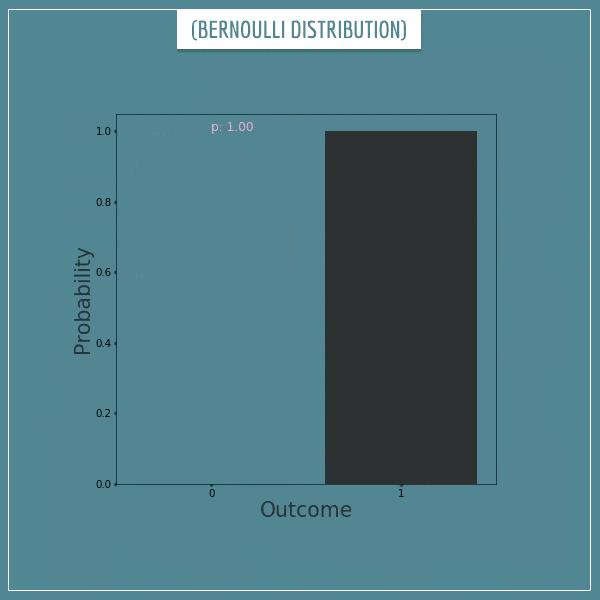

Leave a comment