작업량의 측면에서 해석된 확률 분포간 차이, Wasserstein Distance

Wasserstein Distance는 쉽게 말해 비교 대상이 되는 확률 분포끼리 가지는 유사도를 나타내는 단위로, 물리학에서 정의된 일 ($work = force * distance$)과 비슷한 개념을 사용하여 정의 된다.

출처:link

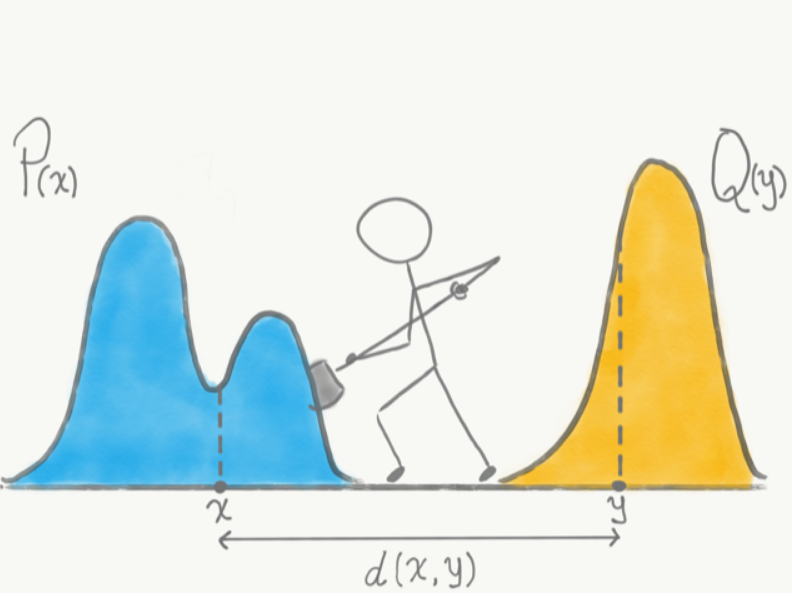
위 그림에서 보는 것 처럼, 두 확률 분포 P(x)와 Q(y)가 있을 때, 확률 분포값을 흙더미로 생각해서 P(x)를 Q(y)처럼 만드는데 필요한 최소한의 일의 양이 Wasserstein Distance 라고 생각하면 된다.

출처:link

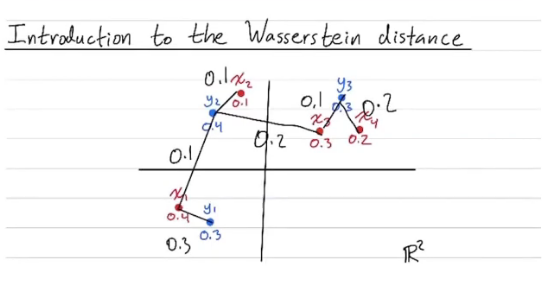
이해를 돕기 위해 위 그림을 보자. 확률 변수 x, y에 대한 확률 질량 함수가 위 그림과 같이 정의 된다고 하면, 빨강 점에 있는 mass 값 (예를 들어 $x_1=0.4$) 을 옮겨서 파란색 mass 값 ($y_1=0.3, y_2=0.4$)을 가지도록 하는 상황을 생각해보자. 얼만큼 옮겼는지는 검은색 라인 위에 표현되어 있다. 옮기는 방식은 여러 방식이 있을 것이고 ($x_1$을 $y_3$ 이나 $y_2$에 옮긴 다든지) 이렇게 옮기는 방식을 아래와 같이 matrix 형태로 표현할 수 있다. 이를 Transport plan이라고 한다.

출처:link

Transport plan은 얼만큼의 mass를 옮길 지 표시된 matrix이고, 여기에 distance를 곱하면 물리학에서 정의한 일의 개념과 같게 된다. Wasserstein distance는 transport plan에 따라 달라지게 되는 총 일의 양 중 가장 작은 값을 뜻한다.

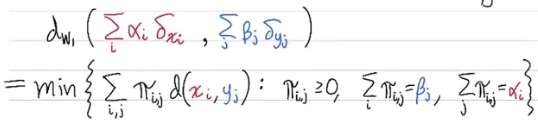출처:link

위 그림에서 $d_{w_1}$ 은 wasserstein distance, $\alpha_i$ 및 $\beta_j$ 는 mass값, $\delta$ 는 kronecker delta 함수이다.

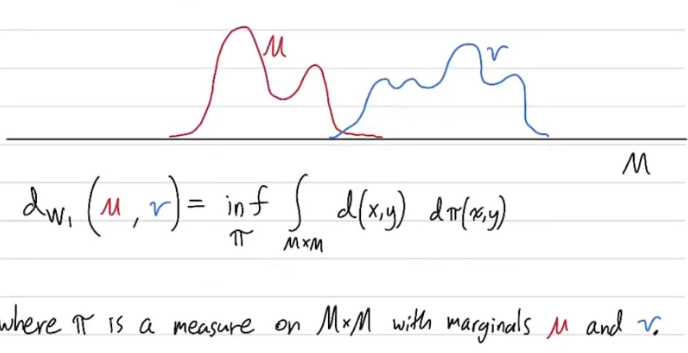
probability density function에 대해 생각해보면 wasserstein distance는 다음과 같이 나타낼 수 있다.

출처:link

여기서 inf는 infimum으로, 가능한 경우의 수가 무한대일 때 그중 하한선을 고르기 위해 정의된 개념이다. 만약 경우의 수가 유한한 경우 최솟값은 explicit하게 구할 수 있으며, 이 때는 minimum값을 사용한다.