Normal-Gamma Distribution
1. Intro
Normal-Gamma distribution은 말 그대로 정규화 된 Gaussian distribution인 Normal distribution과 Gamma distribution을 곱한 형태로, 평균 $\mu$ 과 표준편차 $\sigma$ 가 parameter로 주어지는 Normal distribution에서 표준편차 $\sigma$ 를 Gamma distribution을 따르는 $\tau$ 로 나눠 이를 변수화 한다. 이렇게 하면 정확도(precision)를 확률변수로 포함시킨 확률 밀도함수를 다룰 수 있게 된다. 먼저 Normal-Gamma distribution을 다루기 전에 각각의 pdf인 Normal distribution과 Gamma distribution을 살펴보자.
Normal distribution
우리에게 가장 익숙한 Normal distribution은 잘 아시다시피 평균과 표준 편차 값으로 이루어져있다. univariate인 경우에 대해서 pdf는 다음과 같이 주어진다.
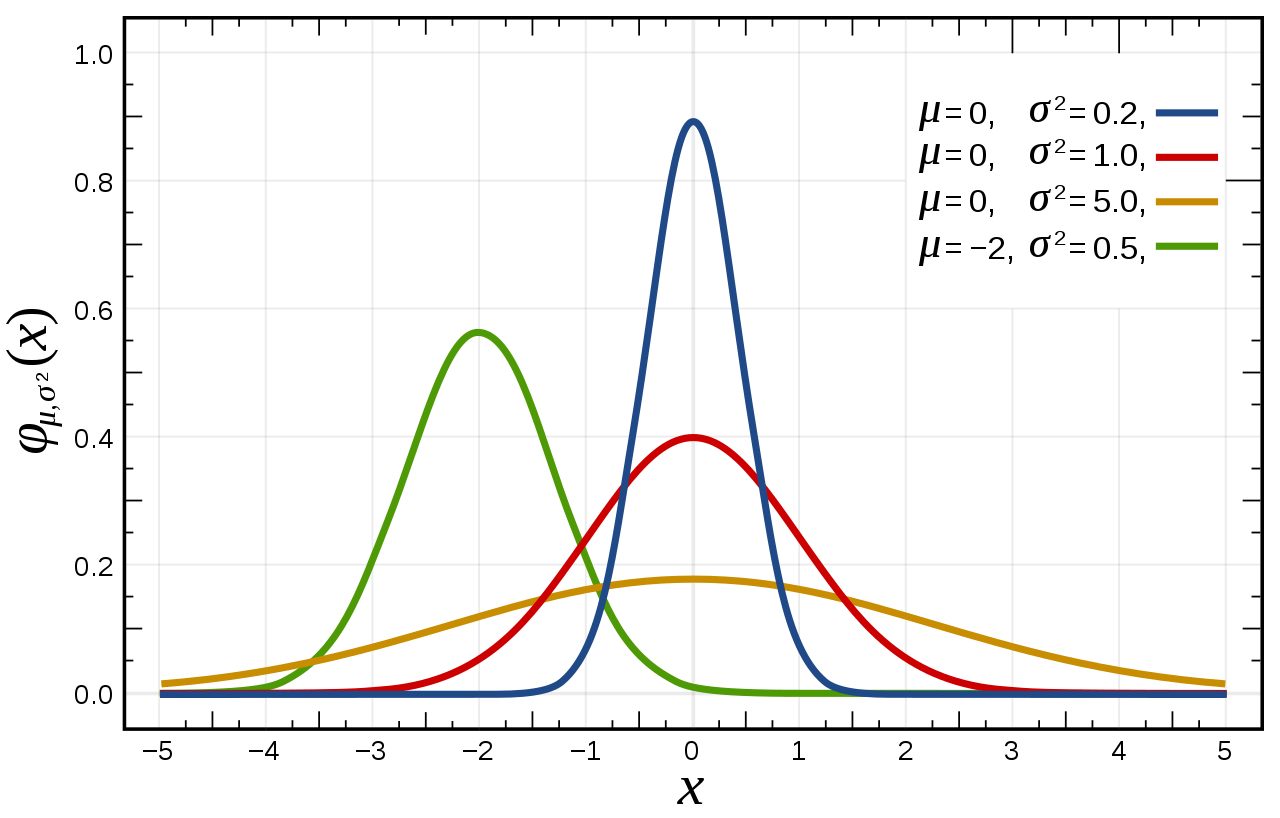
\[\begin{aligned} f(x|\mu,\sigma^2)=\frac{1}{\sigma\sqrt{2\pi}}\exp{}^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \end{aligned}\]사실 너무나도 보편적인(?) pdf 이기 때문에 그래프가 어떻게 생겼는지는 거의 다 알 것이다. Normal distribution의 parameter인 평균값 $\mu$ 를 기준으로 좌우 대칭이며, $\sigma$ 값이 클 수록 그래프가 더 펑퍼짐하게 펴지고, 작을수록 샤프하게 평균값 근처로 모이는 형태이다.
Gamma distribution
Gamma distribution은 Gamma function의 parameter인 a,b를 이용해 표현하며 보통 확률 이벤트가 어떠한 시간 안에 발생할 확률과 같이 Queueing theory 관련 문제를 해결하는데 사용되는 확률 분포이다. 예를 들자면 평균적으로 1달 동안 고장나지 않는 부품을 공장에서 사용하고, 이 부품에 대한 spare가 2개 더 있을 때, 공장이 6개월 동안 고장 나지 않을 확률 (= 3개의 부품이 6개월 동안 버틸 확률)을 구하는 문제가 있다. pdf는 다음과 같이 주어진다.
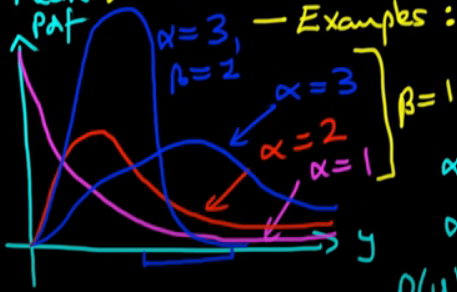
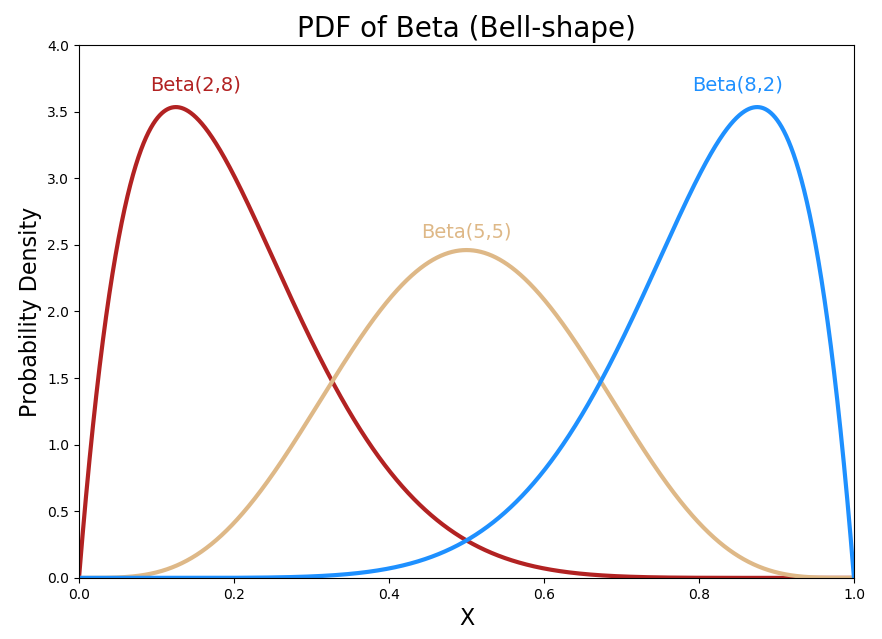
\[\begin{aligned} f(x|\alpha,\beta)=\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x} \end{aligned}\]parameter값인 $\alpha$ 와 $\beta$ 에 의해 그래프는 달라지게 되며, 통상 $\alpha$ 에 의해 개형이 달라지고, $\beta$ 에 의해 y축의 scale이 달라진다고 생각하면 된다. 그래프는 아래와 같다.
 reference:link
reference:link
2. Probability distribution function
이제 두 distribution이 합쳐진 형태를 보자. x, y는 각각 normal distribution과 gamma distribution의 확률 변수이고, y의 경우 normal distribution의 표준편차를 나누는 항으로 들어가서 normal distribution의 precision을 나타내도록 했다.
\[\begin{aligned} x|y&\sim N(x|\mu,\frac{\sigma^2}{y})\\ y&\sim Gamma(y|\alpha,\beta) \end{aligned}\]이 때, joint pdf는 다음과 같다.
\[\begin{align} p(x,y)=p(x|y)p(y)&=N(x|\mu,\frac{\sigma^2}{y})Gamma(y|\alpha,\beta)\\ &:=NormalGamma(x,y|\mu,\sigma,\alpha,\beta)\tag{1} \end{align}\]이 표현식을 해석해보자. Normal distribution의 표준편차를 Gamma distribution의 확률 분포 $y$ 로 나눠서 정규분포의 정확도를 표현하고, (\tau 값이 작을수록 std가 커지기 때문에 정확도가 떨어짐) 뒤에 있는 Gamma distribution은 해당 정확도를 가지는 normal distribution에 scaling 역할을 해준다.
Gamma distribution의 개형에 따라 이 scale의 값은 바뀌게 되며, $\alpha=0$ 인 gamma distribution의 경우 $y=0$ 부근에서 pdf 값이 매우 크기 때문에 이 경우 Normal-Gamma distribution에서는 정확도가 떨어지는(표준 편차가 큰, 무한대인) Normal distribution에 대한 확률 밀도값이 매우 크게 된다. 즉, Normal-Gamma distribution은 기존의 확률변수에다가 정확도라는 확률 변수를 추가적으로 고려하여 정확도가 떨어질 때의 확률 분포, 그리고 정확도가 높을 때의 확률 분포도 표현할 수 있게 해준다.
보통 Queueing theory와 같은 분야의 문제를 풀기 위해 Gamma distribution만 단독으로 사용하는 경우 domain (x축)이 시간, 그리고 y축이 rate (발생 빈도)로 나타내어 사용하곤 하나, Normal-Gamma distribution에서 Gamma distribution의 domain은 시간이 아니라 그저 정확도를 나타내기 위한 변수이니 너무 시간의 개념과 연동시키려고 애쓰지 말자.
한편, 식 (1)의 형태는 gamma distribution 에 대해 해석하면 posterior = likelihood * prior의 형태로, 일반적으로는 posterior을 다시 pdf로 나타내기 위해 normalization을 수행해야 한다. 쉽게 말하면 likelihood * prior로 구한 pdf로 적분했더니 그 값이 1이 나오지 않아 1이 나오도록 조정하는 작업이 필요하다. 그러나 Gamma distribution은 conjugate prior라는 특성을 가지고 있기 때문에 Gamma distribution이 prior로 주어진 경우 likelihood를 곱할 때 나오는 posterior는 별도의 normalization 작업이 필요 없이 Gamma distribution 형태로 나온다.
한편 이 Normal-Gamma distribution은 parameter 4개에 대해서 두개의 변수로 결정되므로 다음과 같이 표현할 수 있다.
3. Posterior density
\[\begin{aligned} \mu'&=\frac{\frac{\mu}{\sigma^2}+\Sigma_{i=1}^{n}x_i}{\frac{1}{\sigma^2}+n}\\ \frac{1}{\sigma'^2}&=\frac{1}{\sigma^2}+n\\ \alpha'&=\alpha+\frac{2}{n}\\ \beta'&=\beta+\frac{1}{2}(\frac{\mu^2}{\sigma^2}-\frac{\mu'^2}{\sigma'^2}+\Sigma_{i=1}^{n}x_i^2) \end{aligned}\](tbd)
4. Usage
멀티 타겟 트래킹에서는 트래킹 해야하는 물체의 여러 면에서 측정치가 얻어진다는 현상이 있다. 그러나 문제는, 이 측정치가 어느 면에서 얻어지는 것인지 알 수가 없다는 것이다. 따라서 이를 해결하기 위해 Normal-Gamma distribution을 이용하여 측정치 방정식을 modelling한 논문이 있는데, 이 경우 측정치가 자동차의 중심에서 어느정도 떨어져있는지를 Normal distribution을 통해 표현하고 그 정확도가 불분명하므로 Gamma distribution을 도입하여 Normal-Gamma distribution의 형태로 측정치 방정식을 모델링하여 문제를 해결한다.


Leave a comment