여러 번의 시행 중 몇 번 성공할 확률? Binomial Distribution

1. Intro

Binomial distribution은 한 번의 시행의 성공/실패에 대한 확률 분포를 나타낸 Bernoulli distribution의 여러 시행에 대한 확장판이다. Binomial distribution에 대한 대표적인 예시는 앞면이 나올 확률이 0.5인 동전을 10번 던졌을 때 x번의 앞면이 나올 확률을 구하는 것이다.

2. Probability density function

한 이벤트의 시행 결과가 다른 이벤트의 결과에 영향을 미치지 않을 때, 이를 독립적인(independent) 시행이라고 한다. 이런 독립적인 시행을 n 번 한다고 했을 때, 성공확률이 p인 이벤트에 대해서 k번 성공했을 때의 probability density function은 다음과 같다.

\[\begin{aligned} P(X=k) = \binom{n} {k}p^k(1-p)^{n-k},\quad 0\le k\le n \end{aligned}\]

보통 probability density function 이면 당연히 x 축에 대하여 적분을 수행하면 그 합이 1이 되도록 normalization을 수행하기 마련이다. 하지만 보통 우리가 처음으로 binomial distribution을 접할 때는 위 수식과 같은 정의만 보고 합이 1이겠거니~ 하고 받아들이는 경우가 많다. 그렇다면 위 수식이 정의역에 대하여 적분 시 합이 1이 되는 이유는 무엇일까?

그 이유는 확률 분포의 이름인 ‘binomial distribution’ 에서 짐작할 수 있다. 왜냐하면 식의 형태가 binomial expansion의 일부를 나타내기 때문이다. $(a+b)^n$ 의 binomial expansion은 다음과 같다.

\[\begin{aligned} (a+b)^n &= a^n + \binom{n}{1}b+ \binom{n}{2}a^{n-2}b^2+\cdots+b^n\\ &=\sum_{k=0}^{n}\frac{n!}{(n-k)!k!}a^{n-k}b^k \end{aligned}\]

여기서 $a=p, b=1-p$ 라고 하면 위 binomial expansion은 그저 $1^n$ 을 $n$ 개의 항에 대해서 나타낸 것에 불과하다. 각 항은 binomial distribution의 probability density (정확히는 probability mass) 이다. 즉,

\[\begin{aligned} \sum_{k=0}^{n}P(X=k) &= \sum_{k=0}^{n}\binom{n} {k}p^k(1-p)^{n-k},\\ &=1 \end{aligned}\]

reference:link

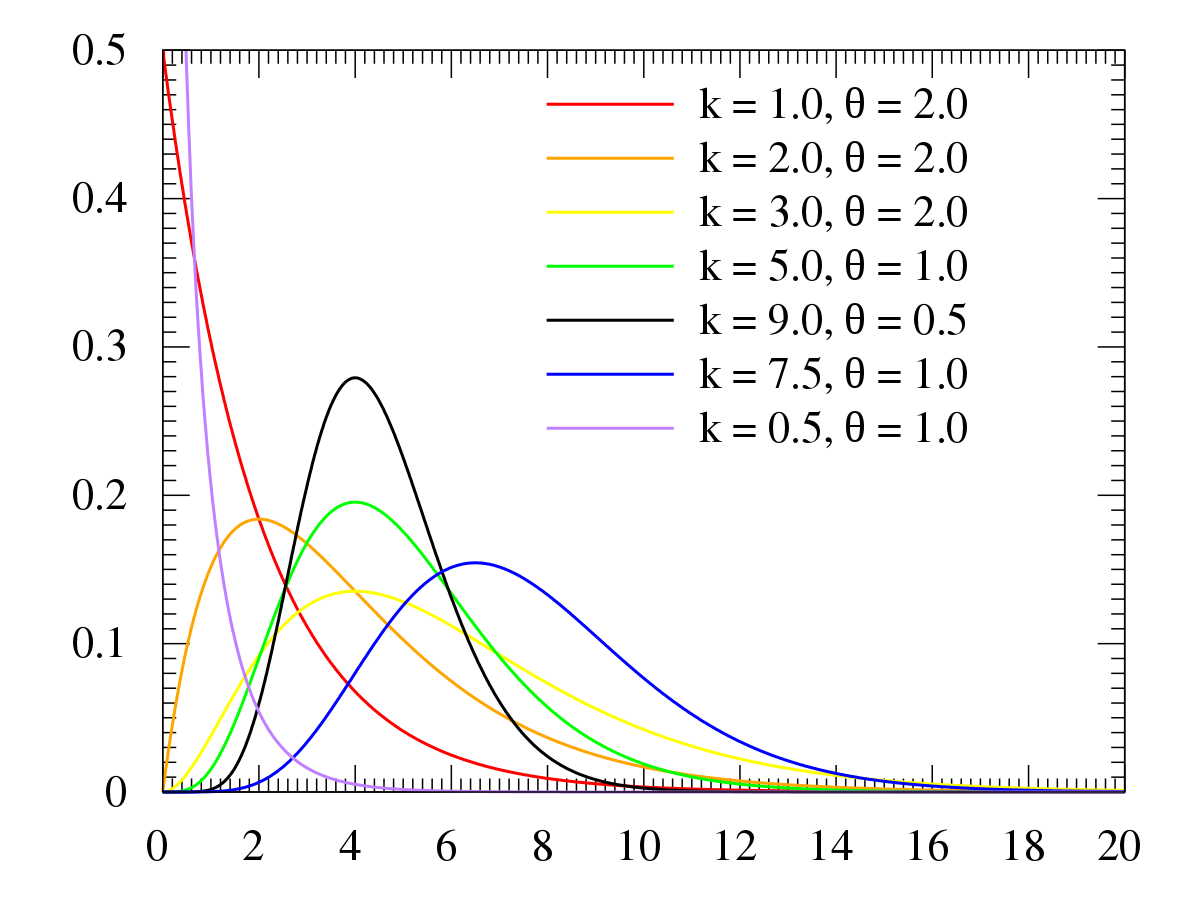
Binomial distribution을 아주 재밌게 시각화 한 장난감(?)도 있다. 구슬을 아래 그림과 같이 떨어트리게 되면 분기점에서 오른쪽/왼쪽으로 나뉘는 두 가지 시행 결과를 가지게 된다. 이러한 분기점을 예를 들어 40번 만난다고 할 때, 어느 한쪽으로 나뉠 확률이 0.5로 같다고 하면 구슬이 쌓여서 생기는 분포는 위쪽에 그림의 파랑색을 닮게 된다.

3. Properties

(tbd, mean variance)

4. Usage

Binomial distribution은 정의역이 ‘횟수’ 에 해당하는 확률분포이다. 이는 나중에 ‘공간’ 을 추가적으로 고려한 확률분포인 Poisson distribution을 다룰 때 사용하게 된다. 이는 레이더에서 감지된 물체의 분포에 대한 모델링에 필수적인 것으로, 레이더의 감지 영역 (Field of view, FOV)에 대해서 트래킹할 물체를 성공적으로 감지/또는 감지 실패 (성공/실패와 같이 두 가지 결과) 하는 경우를 모델링 하기 위해 필요하다. 나중에 설명하겠지만, Poisson distribution은 binomial distribution에서 n을 무한대로 보냈을 때의 분포이기도 하다.