한 이벤트의 발생 확률에 대한 확률 분포, Beta distribution
1. Intro
흔히 알려져 있는 Normal distribution의 경우, 평균이 0이고 그 외에 값에 대해선 표준 편차에 의해 확률 변수 값이 정해진다. 예를 들어 표준 편차가 1인 경우 확률 변수 값이 10일 때 probabiltiy density 값은 매우매우 작은 값을 가질 것이다.
한편, 확률 변수가 0에서 1 사이 값만 가지도록 정의된 확률 분포가 있다. 오늘 소개할 Beta distribution이 바로 그러한 확률 분포이다! 예를 들어 어떤 야구선수의 타율이 0.3에서 0.4 사이에 위치할 확률은 어느 정도나 될까? 또는 한국에서 코로나 확진 비율이 0.3보다 클 확률은? 이렇게 확률이 가지는 확률 밀도 값을 나타내기 위해 Beta distribution이 정의 된다.
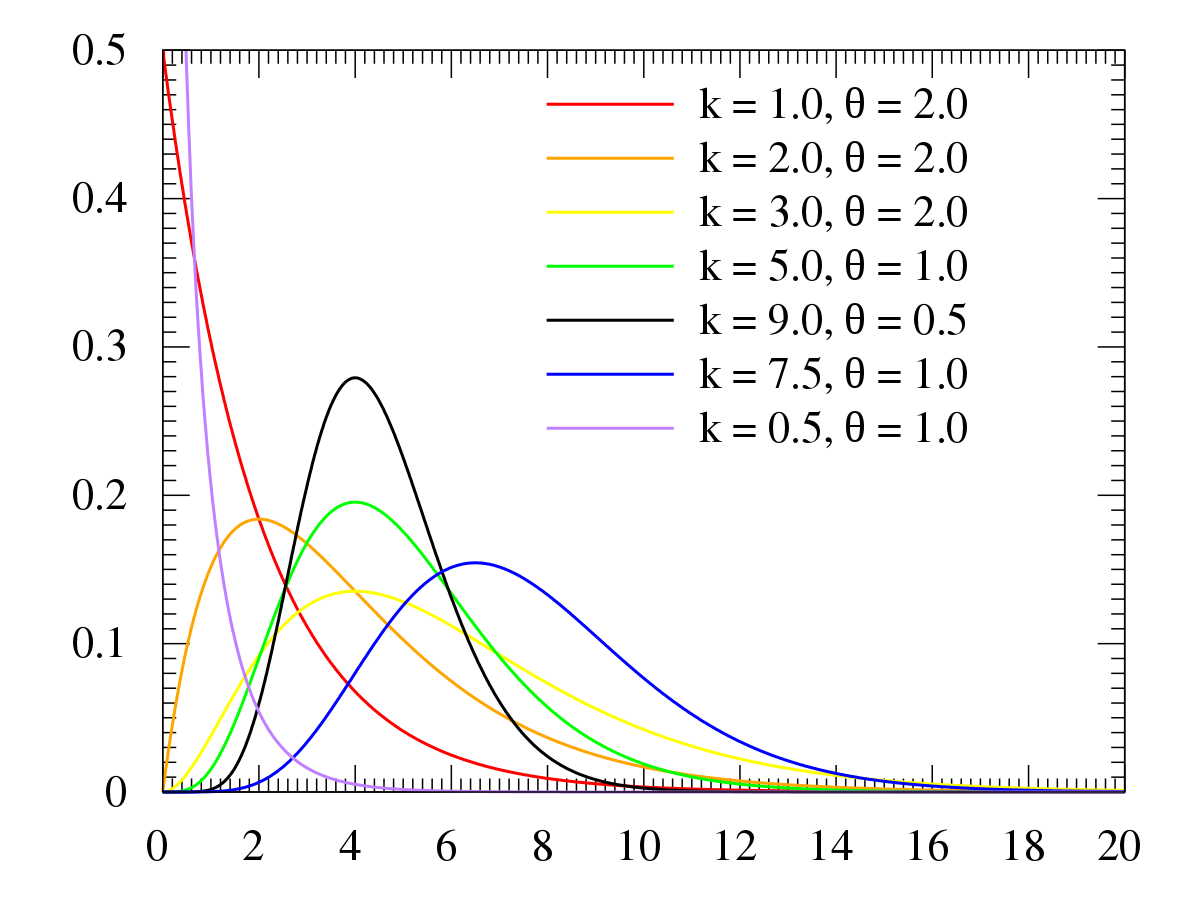
아래 그림을 보면 확률이 가질 수 있는 값인 0에서 1사이에 대해 x축이 정의된 Beta distriubiton을 볼 수 있다. 모양이 여러 개인 이유는 Beta distribution을 결정하는 parameter인 $\alpha$ 와 $\beta$ 때문이다. (빨강 그래프의 경우 $\alpha=2, \beta=8$)
만약 야구선수 타율을 더 잘 설명하는 확률 모델을 정의한다고 하면, 위 세가지 색의 그래프 중에 고른다고 하면 파랑색 보다는 빨강색에 가까울 것이다. 파랑색의 beta distribution의 경우 야구 선수의 타율이 0.5보다 작을 확률을 거의 0에 가깝다고 하는 모델이기 때문이다. (X<0.5 인 정의역에 대하여 그래프의 면적이 매우 작음)
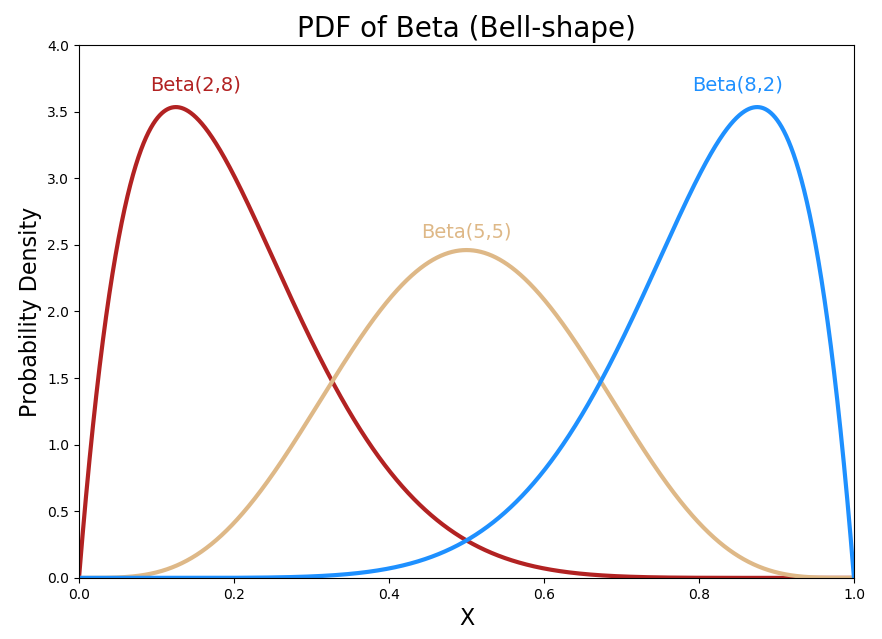x축이 0에서 1사이의 값, 즉 ‘확률이 확률변수’임
2. Probability Density Function
Beta distriubution의 확률 밀도 함수는 다음과 같이 정의된다.
\[\begin{aligned} f_X(x)=cx^{a-1}(1-x)^{b-1} \end{aligned}\]여기서 $c$ 는 normalization constant로 beta function $B(a,b)$ 의 역수에 불과하다. Beta function은 다음과 같이 나타낼 수 있다.
\[\begin{aligned} B(x,y)&=\int_{0}^{1}t^{x-1}(1-t)^{y-1}dt \end{aligned}\]여기서 $t=\sin^2(\theta)$ 라고 하면, 감마 함수의 형태로 나타낼 수 있게 된다.
\[\begin{aligned} B(x,y)&=\int_{0}^{1}t^{x-1}(1-t)^{y-1}dt\\ &=2\int_{0}^{\frac{\pi}{2}}\sin^{2x-1}(\theta)\cos^{2y-1}(\theta)d\theta\\ &=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)} \end{aligned}\]그 이유는 다음과 같다.
\[\begin{aligned} \Gamma(x)\Gamma(y)&=\int_{0}^{\infty}u^{x-1}e^{-u}du\int_{0}^{\infty}v^{y-1}e^{-v}dv\\ &=\int_{0}^{\infty}\int_{0}^{\infty}u^{x-1}v^{y-1}e^{-u-v}dudv \end{aligned}\]여기서 $u=st, v=s(1-t)$ 라고 하면 $dudv=|{det(\mathbf{J})|}dsdt$ 이고, $\mathbf{J} = \begin{bmatrix} \frac{\partial{u}}{\partial{s}} & \frac{\partial{u}}{\partial{t}}\\ \frac{\partial{v}}{\partial{s}} & \frac{\partial{v}}{\partial{t}} \end{bmatrix} = \begin{bmatrix} t & s\\ 1-t & -s \end{bmatrix}$ 이므로, $det(\mathbf{J})=-ts-s+ts=-s$ 이다. 따라서 $dudv=sdsdt$ 가 된다.
\[\begin{aligned} &\int_{0}^{1}\int_{0}^{\infty}st^{x-1}s^{y-1}(1-t)^{y-1}e^{-st-s+st}sdsdt\\ =&\int_{0}^{1}t^{x-1}(1-t)^{y-1}dt\int_0^{\infty}s^{x+y-1}e^{-s}ds\\ =&B(x,y)\Gamma(x+y) \end{aligned}\]결론적으로, Beta distribution은 다음과 같이 나타낼 수 있게 된다.
\[\begin{align} f_X(x) &= \frac{1}{B(a,b)}x^{a-1}(1-x)^{b-1}\\ &=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{a-1}(1-x)^{b-1}\tag{1} \end{align}\]a와 b는 Gamma 함수의 정의역에 해당하므로, 양의 값을 가져야 한다. Gamma function에 대한 설명은 [여기]를 참조하길 바란다.
3. Bionmial distribution과의 관계
식 (1)을 살펴보면, (normalizing factor에 불과한 $\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}$ 를 제외하고) binomial distribution과 형태가 유사한 것을 알 수 있다. Beta distribution이 binomial distribution의 일종의 확장판인 사실은 다음과 같이 확인할 수 있다.
만약에 동전의 앞면이 나올 확률이 어떤지 모르는, 즉 random variable인 상황을 가정해보자. 동전을 5번 던졌는데 3번 앞면이 나오고, 2번 뒷면이 나온 상황에서 앞면이 나올 확률이 0.4, 0.6, 0.8인 세 가지 상황에만 대해서 binomial distribution에 의한 probability density 값은 다음과 같다. 참고로 n번의 시행에 대해서 이벤트가 x번 발생할 확률 분포인 binomial distribution은 다음과 같다.
\[\begin{align} f(x) = \binom{n}{x}p^x(1-p)^{n-x}\tag{2} \end{align}\]
Reference:link
이 결과를 probability mass function으로 나타내면 아래 그림과 같다.
Reference:link
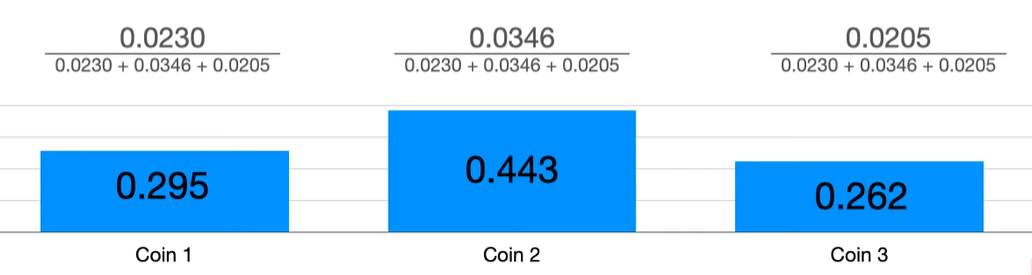
위 그림이 시사하는 바는 동전을 5번 던졌을 때 앞면이 3번 나온 시행에 대해서는 앞면이 나올 확률이 0.6이라고 추측하는 것이 제일 합리적이라는 뜻이다.
이 번엔 동전을 10번 던졌는데 7번 앞면이 나왔다고 해보자. 앞면이 나올 확률을 0부터 1까지 0.1의 간격으로 (0, 0.1, 0.2, $\ldots$, 1) 나눠서 10개의 확률 변수에 대해 동일한 방식으로 probability mass function 으로 나타내면 다음과 같다.
Reference:link
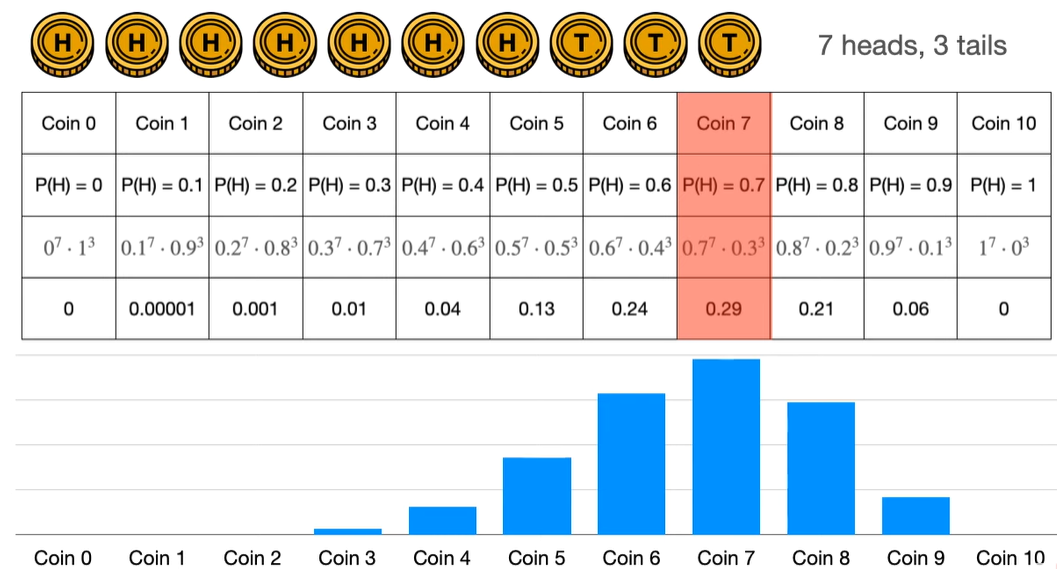
그럼 general 한 확률 변수에 대해서 표현하면 어떻게 될까? 결과는 아래와 같다.
Reference:link
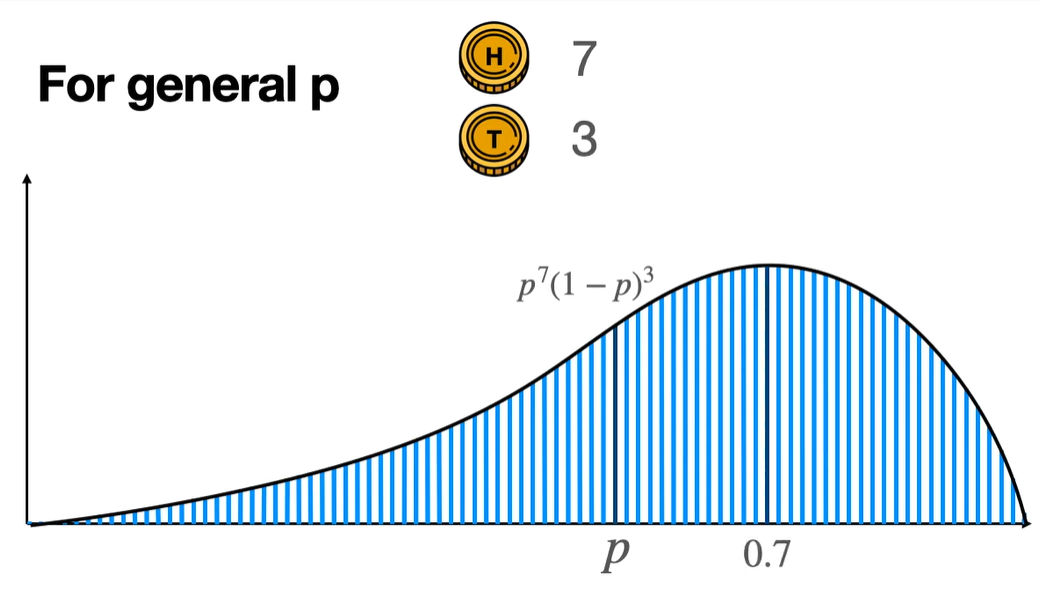
위 확률 분포가 곧 a=8, b=4 일 때의 Beta distribution이다.
여기서 주목해야 할 것은 이벤트의 발생 확률이 parameter로 주어지는 binomial distribution과 달리 beta distribution의 경우 이벤트가 발생할 확률 p가 random variable로 주어진다는 것이다. 대신, beta distribution의 parameter는 지수 부분에 있는 a와 b로 주어진다. 식 (1)과 (2)의 형태를 보면, 지수 부분에 있는 parameter인 (a-1) 과 (b-1)을 이제 어떻게 해석해야 하는지 알 수 있다. 각 이벤트의 발생 횟수라고 생각하면 되는 것이다. $a-1 = 7$ (즉, $a=8$), $b-1 = 3$ (즉, $b=4$)인 위의 예제로 보면 앞면이 7번, 뒷면이 3번인 이벤트가 주어질 때 dirichlet distribution이 주어진 것이다.
Leave a comment