Machine Learning Lecture 8 - PCA & DBSCAN
Overview
PCA
Feature가 여러 개여서 높은 차원으로 표현되는 데이터들에 대해서, 이 데이터들을 잘 표현할 수 있는 주 축들을 설정하고 그 축들이 상대적으로 어느정도로 데이터를 표현하는데 기여하는지를 분석한다. 주 축에 해당하는 것이 데이터의 Covariance matrix의 eigen vector이며 데이터의 표현 정도는 Covariance matrix의 eigen value이다. 데이터의 Covariance matrix에 대해서 eigen 값들을 분석하는 것이 왜 PCA랑 이어지는 지는 선형대수를 곁들여 뒤에 설명한다.
DBSCAN
이렇게 축소한 데이터에 대하여 DBSCAN을 수행하면, 고차원의 데이터에 대해서도 비슷한 부류끼리 묶어서 군집을 형성할 수 있게 된다.
DBSCAN은 특별한 수식으로 이루어진 것은 아니고, 데이터와 데이터 간의 euclidean distance 임계값인 epsilon과 데이터를 이루는 최소한의 멤버 수인 minimum points로 알고리즘이 구성된다. 알고리즘은 다음과 같다.
- 어떤 데이터를 중심으로 epsilon 내에 minimum points 이상의 데이터들이 있다면 그 epsilon을 core points로 한다.
- Core points를 중심으로 새로운 core points를 찾아서 더이상 새로운 core points가 생기지 않을 때 까지 군집을 확장한다.
- Core points 근처에 있으나 epsilon 내에 minimum points 만큼의 수가 확보되지 않은 데이터는 boundary로 처리한다.
- 더이상 새로운 군집이 만들어지지 않을 때 까지 1~3을 반복한다.
- 군집에 속하지 않은 여분의 데이터들을 noise로 처리한다.
Detail
PCA 와 Eigenvalue problem
PCA, 즉 데이터를 설명하는 주 성분은 데이터의 공분산 행렬에 대하여 eigen value와 eigen vector를 구하는 것으로 알려져 있다. 하지만 데이터의 ‘주 성분’이 eigen value와 eigen vector와 무슨 상관이 있는 걸까?
n차원에 있는 데이터에 대해서 Principal Component Axis란 이들을 잘 표현해내는 새로운 축을 의미 한다. 데이터를 잘 표현한다는 것은 어떤 의미일까? 예를 들어 어떤 대학원 신입생 철수와 영희가 선배들을 위해 한 학기 동안의 학식 점심메뉴를 정리한다고 해보자. 철수는 한식/중식/양식/일식/베트남식/멕시코식 등으로 분류를 했는데 영희는 해당 음식이 학교 식당 중 어느 식당에서 조리되었는지로 분류했다고 하자. 철수의 데이터를 보면 음식 메뉴가 어떻게 분포되어 있는지 어느정도 짐작을 할 수 있었지만, 하필 식당이 하나 밖에 없는 학교라 영희의 데이터로는 메뉴에 대해서 아무런 정보도 얻을 수 없었다.
사실 우리가 똑같은 상황에 처하더라도 철수처럼 메뉴를 분류할 것이지, 영희처럼 바보같은 짓은 하지 않을 것이다. 즉, 우리는 어떤 데이터들을 분석할 때 이미 직관적으로 그 분포를 잘 알 수 있는 범주를 설정하며 살아간다. 와인이라면 색상이나 맛으로 분류하지, 병모양으로 구분하지는 않는다. 롤 챔피언이라면 탱커/딜러/힐러/브루저/메이지로 구분하지 남자/여자로 구분하지 않는다. (물론 남자/여자로 구분해놓은 짤도 있는데 별 쓸모가 없다…)
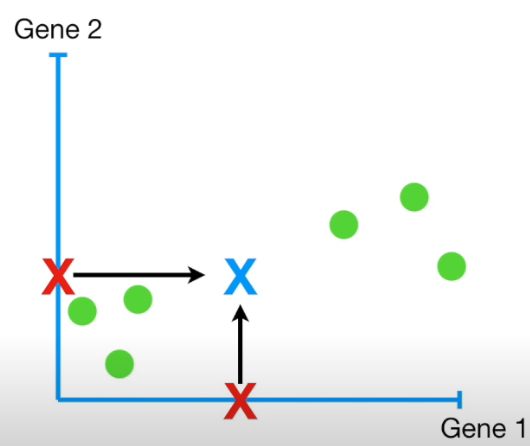
그럼 이제 데이터를 잘 나타내는 principle component axis를 찾아보기 위해 problem definition을 다음과 같이 설정한다 : 데이터를 principle component axis와 평행한 vector w로 projection 시킬 때 projection error를 최소화 시키는 w를 찾자. 데이터를 온전히 표현하기 위해 몇 개의 principle component axis가 필요할지는 나중에 생각하고 (직관적으로는 n차원 데이터라면 n개의 axis가 필요할 것이라 생각된다.) vector w의 시점을 PCA축이 모이는 원점으로 설정하기 위해 다음과 같이 데이터를 변환시키자. 처음에 PCA축과 평행하게 설정한 w의 시점이 원점이 되었으므로, 이제 w를 PCA축으로 보면 된다.
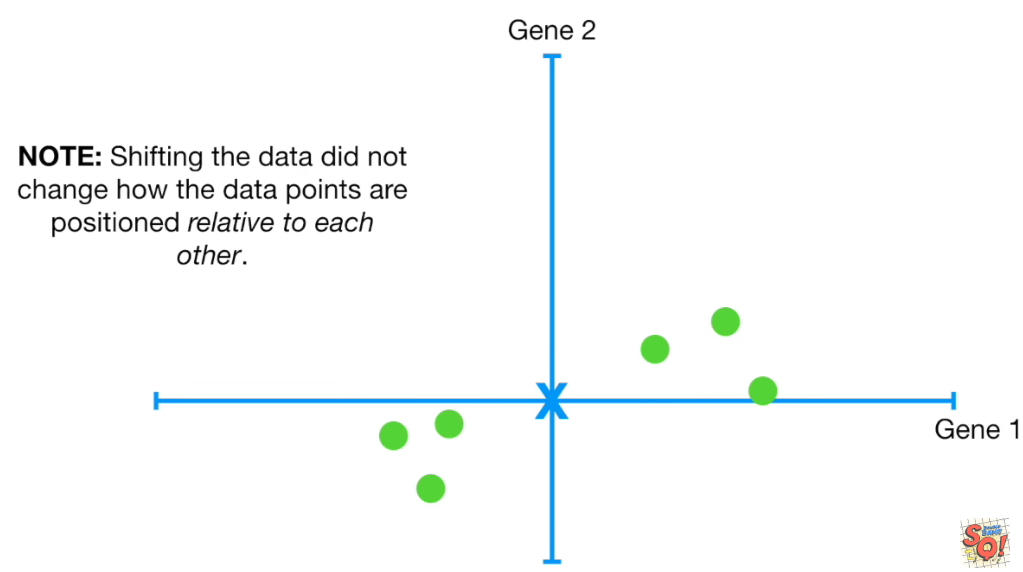
데이터를 벡터로 생각할 때, 평균값을 빼고 나면 데이터는 모두 원점이 (0,0)인 좌표로 평행이동 될 것이다. 각 벡터를 행백터로해서 차곡차곡 행렬의 형태로 나타낼 때 이를 centered data matrix 라고 한다. 아래 그림은 중심이 (0,0) 으로 바뀐 데이터를 나타낸 것이다.
reference-Youtube:StatQuest
reference-Youtube:StatQuest
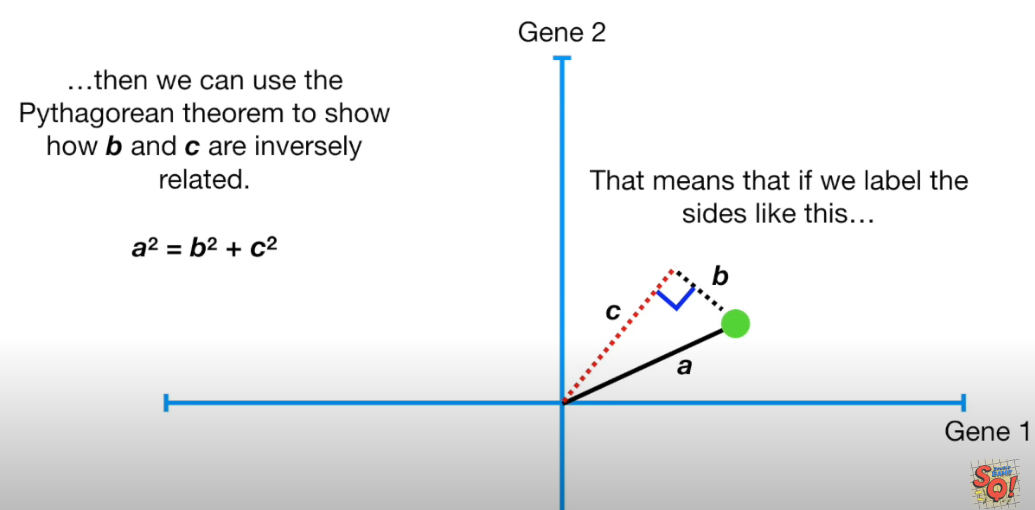
projection error는 projection된 벡터의 길이가 최대일 때이다. (피타고라스 정리!) 아래 그림과 같이 말이다. (a가 개별 데이터를 벡터화 한헋, c가 projection 된 길이, b가 projection error)
reference-Youtube:StatQuest
이제 모든 데이터에 대해 projection error의 합을 최소로 하는 vector w를 구하면 principle axis가 나올 것이다. 여기서 projection error의 합이 최소가 되는 것은 vector w에 projection 시킨 값의 제곱들을 모두 합한 것(S라고 하자)이 최대가 되는 것과 같다.
만약 vector w가 단위벡터라면 내적만으로도 projection을 구할 수 있다. 즉, Centered data matrix를 X라고 할 때 모든 데이터를 w로 내적한 결과는 Xw이므로 $S = (Xw)^TXw = w^TX^TXw$ 가 된다. 여기서 Centered data matrix는 평균 값을 뺀 데이터로 구성되어있다는 사실을 눈치챈다면, $X^TX$ 를 $\frac{1}{n-1}$ 로 나눈 값이 데이터의 공분산 행렬 C임을 눈치챌 수 있다.
결국 위에서 정의한 problem definition은 다음과 같이 정리된다. 데이터의 Covariance matrix C가 주어질 때, $w^TCw$를 최대화하는 단위 벡터 w를 구한다. 이는 제약조건 $|w|=1$ 이 있으므로 라그랑주 승수법(Lagrange multiplier)을 알고 있다면 쉽게 풀 수 있는 최적화 문제이다. Lagrange multiplier을 사용하면 아래의 값을 최대화 시키는 문제가 된다.
\[\begin{aligned} \mathbf{w^TCw-\lambda(w^Tw-1)} \end{aligned}\]이를 $\lambda$와 w에 대하여 편미분 하면 $\mathbf{Cw-\lambda w}=0$ (Eigenvalue와 Eigenvector를 구하는 문제) $\mathbf{w^Tw-1=0}$ 이다. 이 때 최댓값은 $\lambda$ 이므로 n차원 데이터의 공분산 행렬C가 주어질 때 다음을 알 수 있다.
- 공분산 행렬 C에 대한 n개의 Eigen vector는 Principal Component Axis이다.
- 공분산 행렬 C에 대한 n개의 Eigen value를 비교하여 어떤 축이 정보를 잘 나타내는지 비교할 수 있다. (이를 Scree plot으로 나타내곤 함)
참고로 보통 Scree plot은 아래처럼 생겼다.
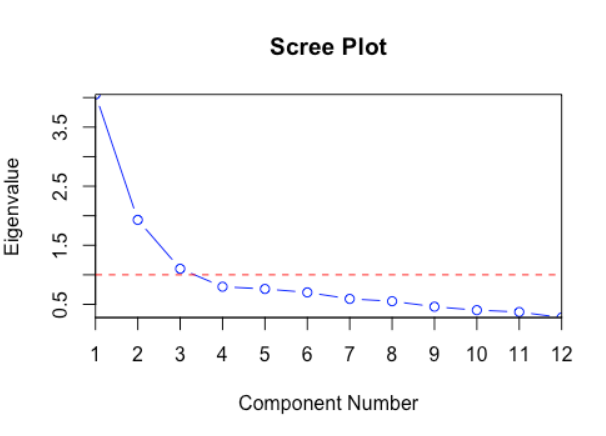
위의 그래프를 해석하자면 12차원 데이터를 표현할 때 상대적으로 Eigenvalue 3개 정도면 데이터의 손실이 적은 편이니, 각 Eigenvalue에 해당하는 eigen vector를 PCA로 설정하여 3차원으로 정보를 축소시키면 합리적일 것이다.
Leave a comment