Machine Learning Lecture 7 - Support Vector Machine

Support Vector Machine

Overview

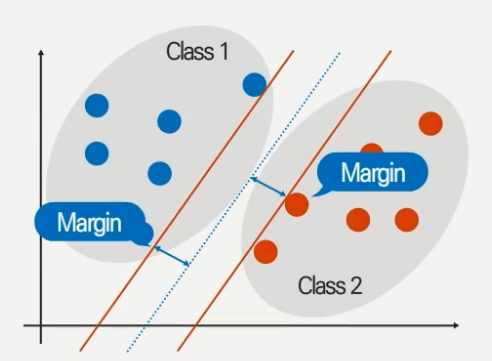
Support Vector Machine은 Decision tree나 Naive bayes와는 달리 비선형적이고 고차원의 공간에서도 높은 classifier 성능을 보여준다. SVM의 원리는 아래 그림과 같이 데이터를 나누는 파랑색 기준선 (hyperplane)과, hyperplane과 같은 기울기를 가지며 최 외각 데이터를 지나는 주황색 선 (support vector)간의 거리인 margin 값을 최대화하도록 hyperplane을 설정하는 것이다.

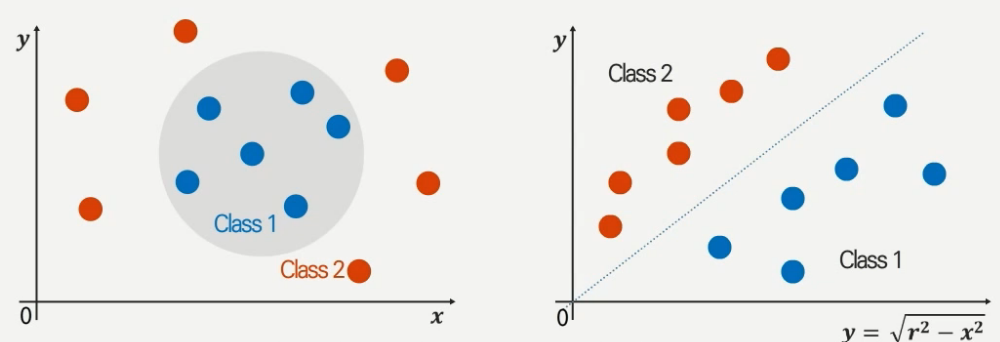
만약 아래 그림과 같이 데이터의 비선형성으로 인해 분류가 쉽지 않은 상황이라면, 데이터를 다른 형태로 mapping 시키는 방식이 있다. Mapping function은 여러가지 형태가 있으며 대표적인 방식으로 polynomial, radial kernel 형태를 가지는 mapping function을 사용할 수 있다.

Detail

Maximum Margin Classifier

사실 위에서 설명한 개론에 있는 그림은 misclassification을 배제하는 것을 전제로 한다. 하지만 misclassification을 허용하지 않을 때는 분류기가 아래 그림처럼 outlier에 의해 영향을 많이 받는 다는 문제가 있다. 그렇게 되는 경우 margin이 적어지게 되어 합리적이지 못한 hyper plane이 설정된다는 문제가 있다.

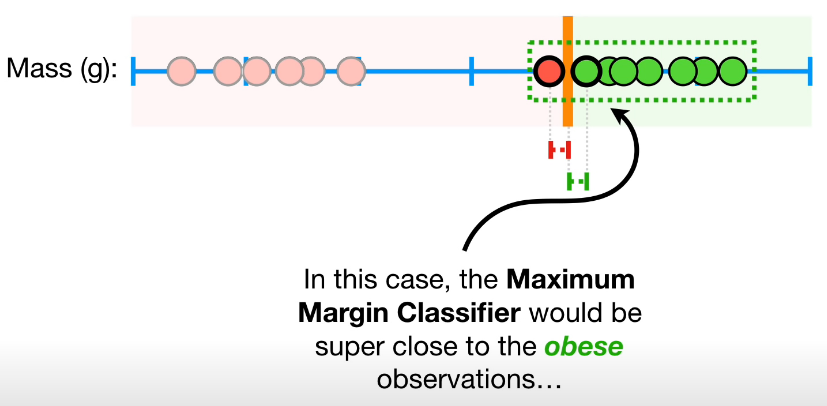reference:Youtube:StatQuest

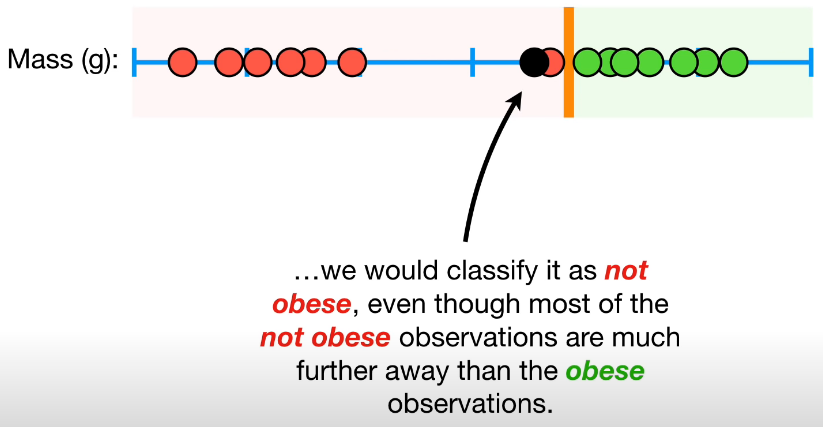reference:Youtube:StatQuest

Support Vector Classifier

따라서 misclassification을 어느정도 허용하는 선에서 support vector를 선정하는 것이 필요하다. 여기서 misclassification을 어느정도로 허용하는 것이 좋을지는 cross validation (직접 다 해봐서 비교함.)을 통해 검증하고, 이 때 최 외각의 데이터를 support vector라고 한다.

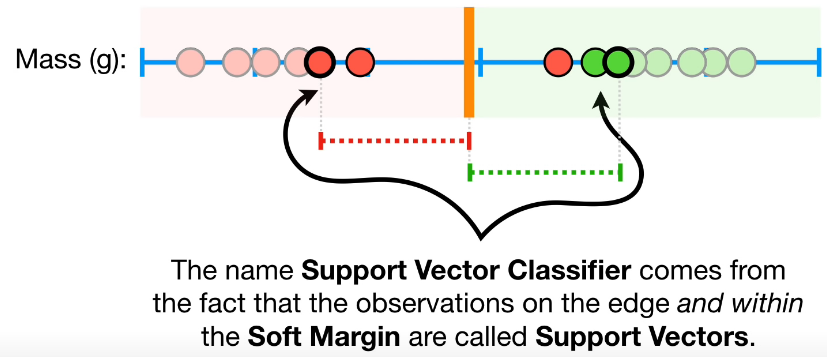reference:[Youtube:StatQuest]

Kernel trick

Kernel trick은 위의 overview 부분에서 데이터를 단순하게 linear regression으로 분류할 수 없을 때 사용하는 방식이다. Kernel trick이 필요해지는 순간을 유도하는 과정은 여기를 살펴보면 된다. (다행히 scikit-learn 패키지에 SVM을 간단하게 활용할 수 있도록 누군가가 Wheel을 잘 invent 해놓으셨지만, 이를 실제로 구현하려면 부등식이 포함된 최적화 문제를 풀 줄 알아야한다.) 여기서는 Kernel trick이 왜 필요한지, 그리고 무슨 역할을 하는지를 간단하게 설명하겠다.

먼저 데이터가 아래 그림처럼 하나의 선으로는 간단하게 구분할 수 없도록 분포되어 있을 때를 보자.

reference:Youtube:StatQuest

이럴 때는 x값(dosage)의 제곱을 다른 차원에 가지도록 데이터의 차원을 높여서 1차원의 데이터를 2차원의 데이터로 옮겨서 최적화 문제를 풀면 된다. 그림으로 표현하면 아래와 같다.

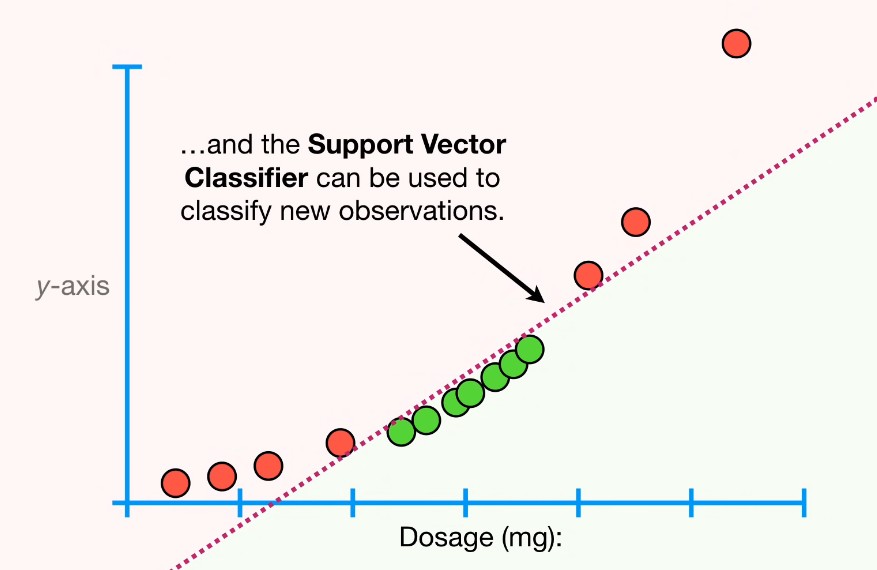reference:Youtube:StatQuest

즉 데이터가 어떤 차원에서 linear regressor에 의해 구분되지 못하는 상황이라면, 더 높은 차원으로 transform시켜서 linear regressor를 구해 분류하면 된다. 데이터가 더욱 복잡하게 분포되어있다면, 더더욱 높은 차원으로 보낼수록 분류 성능이 좋아질 것이라고 유추할 수 있다.

그렇다면 무한대 차수로 보내면 어떻게 데이터가 분포되어 있든 잘 분류를 할 수 있겠네? 라고 생각할 수 있다. 하지만 무한대 차수를 코드로 구현하는 것은 불가능하다. 왜냐하면, 먼저 무한대 차원을 표현하도록 자료형을 구현할 수 없을 뿐더러, 이를 감안해서 적당히 10차원으로 타협하고 최적화 문제를 푸는 과정에서 10차원에 대한 내적을 계산할 때도 많은 연산량을 잡아먹게 된다.

여기서 갑자기 내적이 등장하는 이유는, 결국에 우리가 SVM을 구현하기 위해 마지막으로 얻게 되는 경계선이 내적으로 표현되기 때문이다. 아래 그림을 보면 왜 내적이 등장하는지 알 수 있다.

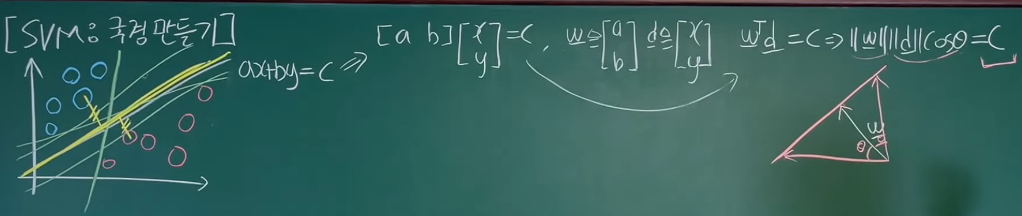reference:Youtube:혁펜하임

따라서 우리가 분류기의 성능을 끌어올리기 위해서 고차원으로 데이터를 변환할 수록, 변환에 걸리는 메모리와 연산시간도 필요하게 된다. 그러니 kernel trick을 사용하면 무한의 차원으로 끌어올리는 계산도 한큐에 된다! Kernel의 종류는 많지만, 여기서는 radial kernel로 설명하겠다.

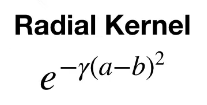
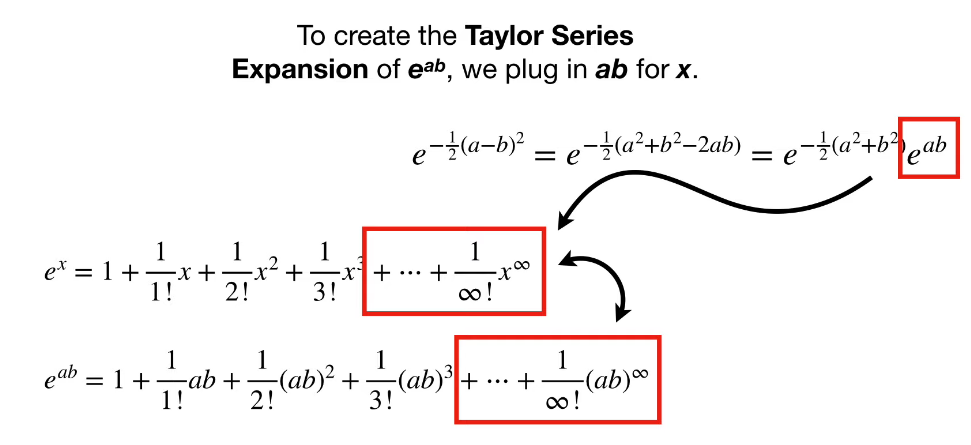
Gamma 값이 0.5인 Radial kernel에 대해서, taylor expansion을 활용하면 아래와 같이 식을 유도할 수 있다.

reference:Youtube:StatQuest

reference:Youtube:StatQuest

즉, radial kernel값을 계산만 하면 이는 무한대의 차원에서 데이터의 내적을 계산하는 것이 되기 때문에 SVM에서 radial kernel을 사용하면 분류가 까다롭게 분포된 데이터에 대해서도 아주 이쁘게 분류를 할 수 있게 된다. 아래 그림과 같이 말이다. (gamma 값이 분류 성능에 대한 튜닝 parameter로 작용한다는 것을 볼 수 있다.)

reference:Youtube:Visually Explained

reference:Youtube:Visually Explained

우리는 이제 opensource로 만들어진 SVM을 API문서만 참고해서 사용하면 된다.