Machine Learning Lecture 5 - K Nearest Neighbors

Overview

Target이 정해져 있는 지도 학습 (Reference 값이 이미 정해져 있음) 예를 들어 결정사에서 사람의 학벌, 페이, 키 등의 속성으로 1군~N군을 분류된 reference를 보유한다고 하자. 신규 유입된 회원에 대해서 속성에 대한 distance를 K 개의 주어진 데이터와 비교하여 제일 많은 비중을 차지한 쪽으로 몇군인지 정하는 방식이다. 단 속성에 따라 값의 범위가 차이가 많이 나는 경우 (키는 보통 150 ~ 190, 페이는 1,000,000 ~ 10,000,000) 정규화를 통해서 비슷한 범주로 만들어놓고 model을 fit 시킨다.

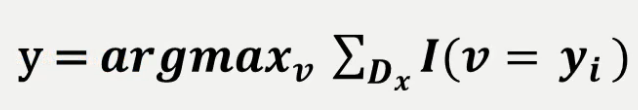
KNN은 기본적으로 분류를 하기 위하여 탄생된 알고리즘이므로 분류에 해당하는 모든 종류의 사업에 적용이 가능하다. 심지어는 얼굴인식이나 글자 인식에도 KNN이 사용될 수도 있고 한정된 상품의 개수가 있다면 가장 적절한 상품 추천 시스템에 적용이 될 수도 있다. KNN에 회귀분석을 결합하여 KNN Regressor를 사용하면 연속값도 예측이 가능하다.

Classification Report 해석법

아래는 150개의 Iris flower(붓꽃)의 5가지 속성에 따라 종류를 구분한 150개의 데이터셋에 대하여 k=20인 (보통 5정도로 잡는 것 같으나, 일부로 오답률을 높이기 위해 높게 잡음) KNN 분류기를 학습시킨 결과이다.

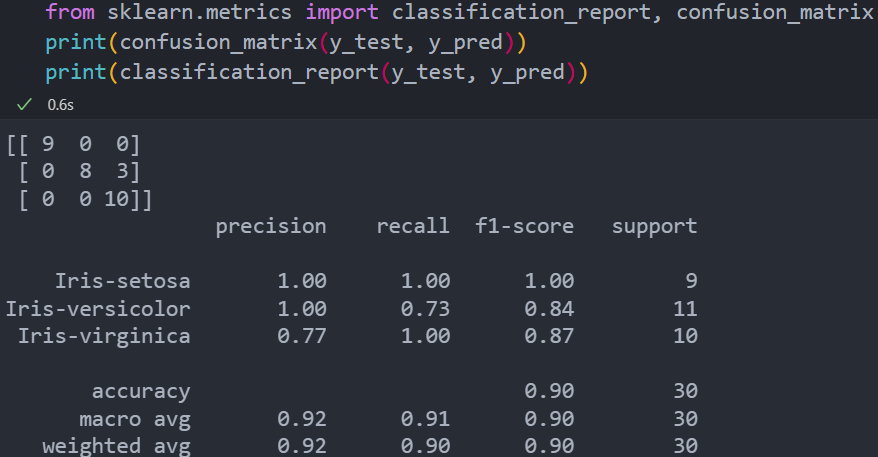
Confusion Matrix

먼저 위 그림에서 confusion matrix가 3 by 3인 행렬인 것으로 보아, 분류된 라벨이 3개인 것으로 보인다. 그리고 confusion matrix의 (i,j) 성분은 Label i가 Label j로 분류된 수를 말한 것이다. 따라서 한 행을 모두 합한 수는 실제로 Label이 i인 데이터의 수를 말하는 것이다. 또한 diagonal 성분은 Label i를 Label i 로 분류한 횟수를 뜻하는 것이므로 올바르게 분류된 데이터 수를 말하는 것이고, off-diagonal 성분이 많을 수록 데이터의 분류결과가 잘못된 경우가 많다는 뜻이다. 라벨이 a, b, c가 있다면 위 결과로 봤을 때 label b의 경우 label c로 3번 비정상적으로 분류된 것을 볼 수 있다.

Preicison

Precision은 model에 의해 label X로 분류된 데이터 중, 실제로 label X인 데이터의 비중을 말한다. Iris-virginica의 경우 Iris-versicolor의 데이터 중 3개가 추가로 Iris-virginica로 잘못 분류되었기 때문에 총 13번의 분류 중 10번만 맞혔다. 따라서 precision = 10/13 * 100 = 77%인 것이다.

Recall

실제로 Label X인 데이터 중, model의 분류 결과가 Label X인 비중을 뜻한다. Iris-versicolor의 경우 실제로 11개가 있지만 그 중 8번만 제대로 분류되었기 때문에 8/11 * 100 = 73%가 된다.

F1-score

Precision 과 Recall의 harmonic mean으로 아래의 수식과 같다.

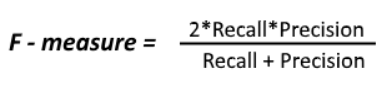
Support

Support는 실제로 분류되어야 할 데이터의 수를 의미한다.

Accuracy

Accuracy는 말 그대로 모든 데이터 개수 중 Label이 제대로 분류 된 데이터의 수를 의미한다. 30개 중 3개만 잘못 분류되었기 때문에 accuracy는 0.9이다.

Macro Avg

Macro average에 있는 각 항들은 precision, recall, f1-score끼리 다 더하고 데이터 Label 종류 수만큼 나눈 것이다. 예를 들어 f1-score의 macro avg는 (1 + 0.84 + 0.87) / 3 = 0.9이다.

Weighted Avg

Weighted Avg는 데이터의 편중을 고려한 지표이다. 30개의 데이터 중 Iris-setosa, Iris-versicolor, Iris-virginica의 갯수는 각각 9, 10, 11이므로 weight는 0.3, 0.33, 0.36이 된다. 이 weight를 바탕으로 f1-score의 weighted average를 구해보면 1 * 0.3 + 0.84 * 0.33 + 0.87 * 0.36 = 0.90 이 된다.

위와 같이 여러가지 지표가 있는 경우는 데이터셋의 분포에 따라 분류 결과의 성능 측정을 고려해야 하기 때문이다. 예를 들어 Iris 데이터 중에서 희귀종으로 분류된 데이터를 가지고 실제 희귀종을 제대로 분류하는 문제에 대해 생각해보자.

Input 데이터 셋에 실제로 희귀종인 꽃이 3개 밖에 없었을 때, 3개 중에 1개밖에 제대로 분류하지 못했다면 희귀종 label에 대해 recall 값이 매우 낮게 나와 f1-score이 낮아질 것이다.

따라서 f1-score에 대해 macro avg를 했을 경우 낮은 값이 나와 ‘학습을 잘못 시켰나?’ 라고 잘못된 평가를 내릴 수 있기 때문에 weighted avg도 필요하게 된다.