Machine Learning Lecture 3 - Linear Regression

Linear Regression

Overview

Linear Regression은 말 그대로 충실하게 ‘선형’(방정식)으로 회귀 시킨다는 뜻이다. 데이터가 있을 때, 이들의 분포를 하나의 선형 방정식으로 대표하겠다는 뜻이다. 그럼 선형 방정식이란 무엇일까? 우리가 흔히 중고등학교 때부터 그려오던 2차원에서는 선이겠지만, 차원이 높아지면 어떻게 될까? 예상한대로 3차원에서는 평면이 선형 방정식에 해당한다. 즉, 선형 방정식은 해당 방정식의 차수가 최대 1을 넘지 않는 식을 말한다. 아래 식들은 모두 X, Y에 대해서 선형방정식이다.

\[\begin{aligned} Y=aX+b \end{aligned}\tag{1}\] \[\begin{aligned} a^2X + b^2Y = 1 \end{aligned}\tag{2}\] \[\begin{aligned} \frac{X}{a} + \frac{Y}{b} = 3 \end{aligned}\tag{3}\]

물론 식 (2)와 식 (3)은 a,b에 대해서는 선형 방정식이 아니다.

제어를 공부했던 사람이라면 ‘선형 시스템’에 나타나는 ‘선형’과 선형 방정식에 나타나는 ‘선형’을 헷갈릴 수 도 있다. 제어의 관점에서는 위 세 개의 식중 어느 식도 선형 시스템이 아니다. 갑자기 헷갈리기 시작한다면 이 부분은 잠시 넘어가기로 하고 나중에 여기를 참고해보자.

Simple Linear Regression

좋다. 선형방정식으로 데이터를 나타낸다고 하니까 일단 데이터의 분포를 제일 먼저 $Y = AX+b$ 로 나타내 보기로한다. 이 형태는 Y가 변수 X 하나로만 결정되는 모델이니까 평균 온도에 따른 아이스크림 판매량, 키에 따른 몸무게와 같이 어떤 데이터 (아이스크림 판매량, 몸무게)를 결정짓는데 있어 데이터가 하나의 차원, 또는 하나의 종류 (평균 온도, 키) 만 있으면 된다는 의미이다.

데이터 (X, Y)의 쌍이 주어질 때 둘 간의 관계를 잘 나타내는 A, b는 어떻게 선정할 것인가? 어떤 사람이 $A = A_0$, $b = b_0$ 라고 선정했다면, 우리는 그 모델이 얼마나 잘 맞는지 채점할 때 실제로 측정한 $Y_0$ 값에서 $\hat{Y_0}(=A_{0}X + b_{0})$값을 뺀 값인 $Y_0-\hat{Y}_0$를 ‘오차’로 생각해서 이 값이 클수록 A와 b를 잘못 선정했다고 생각할 것이다. 근데 여기서 이제 데이터의 갯수가 1000개가 있다고 하면 오차의 총합은 아래와 같다.

\[\begin{aligned} \sum_{i=1}^{1000}(Y_i-\hat{Y_i}) \end{aligned}\]

근데 여기서 오차가 +1, -1 이런 식으로 같은 크기를 가지고 부호가 반대인 형태로 계속 나오면 오차의 총합이 0이 되기 때문에 흔히 오차의 제곱합을 채점 결과로 많이 사용한다. 이를 n개의 데이터에 대하여 표현하면 아래와 같다.

\[\begin{aligned} \sum_{i=1}^{n}&(Y_i-\hat{Y_i})^{2}\\ =\sum_{i=1}^{n}&(Y_i-AX_i-b)^{2} \end{aligned}\tag{4}\]

바로 (4)가 우리가 최소화 해야되는 cost function이 되는 것이며, 이는 Gradient Descent 방식으로 찾을 수 있다. Gradient Descent란 A와 b에 따라서 식 (4)가 가지는 값을 마치 산등성이 처럼 생각하여 매 순간 A와 b를 조금씩 변화시키면서 편미분으로 구한 기울기를 따라 발걸음을 내딛어가며 최소값을 찾는 방식이다. 식 (4)를 각각 A와 b에 따라 편미분한 결과는 아래와 같다.

\[\begin{aligned} \frac{\partial(4)}{\partial A} &= -2\sum_{i=1}^{n}X_{i}(Y_{i}-AX_{i}-b) \end{aligned}\tag{5}\] \[\begin{aligned} \frac{\partial(4)}{\partial b} &= -2\sum_{i=1}^{n}(Y_i-AX_i-b) \end{aligned}\tag{6}\]

따라서 Gradient Descent 알고리즘은 간단하게 아래와 같다.

1. $A_i$, $b_i$ 을 적당히 선정한다.
2. 식 (5)와 (6)을 통해 $A_{i+1} = A_{i} - \eta\frac{\partial(4)}{\partial A}$, $b_{i+1} = b_{i} - \eta\frac{\partial(4)}{\partial b}$ 를 계산한다.
3. (4)의 값이 어떠한 값으로 수렴할 때 까지 2를 반복한다.

Multiple Linear Regression

사실 위의 방식만 이해를 했다면 여기서부터는 파생에 불과하다. Multiple Linear Regression이란 Y를 결정하는 값으로 X 하나만 있는게 아니라 $X_1, X_2, \ldots, X_n$ 이 있다는 뜻이다. 즉 $\beta_0, \beta_1, \ldots, \beta_n$ 에 대한 선형 방정식

\[\begin{aligned} Y = \beta_0 + \beta_1X_1 + \ldots + \beta_nX_n \end{aligned}\]

를 근사시키는 것 뿐이다. 만약에 Y를 결정하는 값이 어떠한 한 종류의 값이 아니라면 simple linear regression 보다 더 나은 성능을 보일 수 있다.

Polynomial Regression

Polynomial regression은 $\beta_0, \beta_1, \ldots, \beta_m$ 에 대한 선형 방정식

\[\begin{aligned} Y = \beta_0 + \beta_1X_1 + \beta_2X_1^2 + \beta_3X_1^3 + \beta_4X_2^2 + \beta_5X_1X_2 + \ldots + \beta_mX_1^aX_2^b \end{aligned}\]

처럼 다항식 형태로 거듭제곱 된 계수가 추가된 형태로 데이터를 근사하는 것이다. 저차원에서는 데이터가 비선형 이지만, 적절히 데이터를 조합하여 만든 고차원에서는 저차원에서 표현됬을 때 보다 선형성이 생기는 원리를 이용한 것으로, 마치 SVM의 kernerl trick을 연상하게 한다.

Prevent Overfitting

Data가 주어질 때 모든 데이터에 대해서 훈련을 하는 것 보다는 부분만 떼서 하는게 과적합 측면에서 더 좋은 결과를 나타낸다. 과적합을 방지하는 방식에는 k-fold cross validation, regularization이 있다.

k-fold Cross Validation

k fold validation은 전체 데이터를 k 개로 나눠 train용 데이터와 test용 데이터가 다른 k 번의 결과를 고려하는 방식이다. 아래 그림을 보면 한 방에 이해할 수 있다.

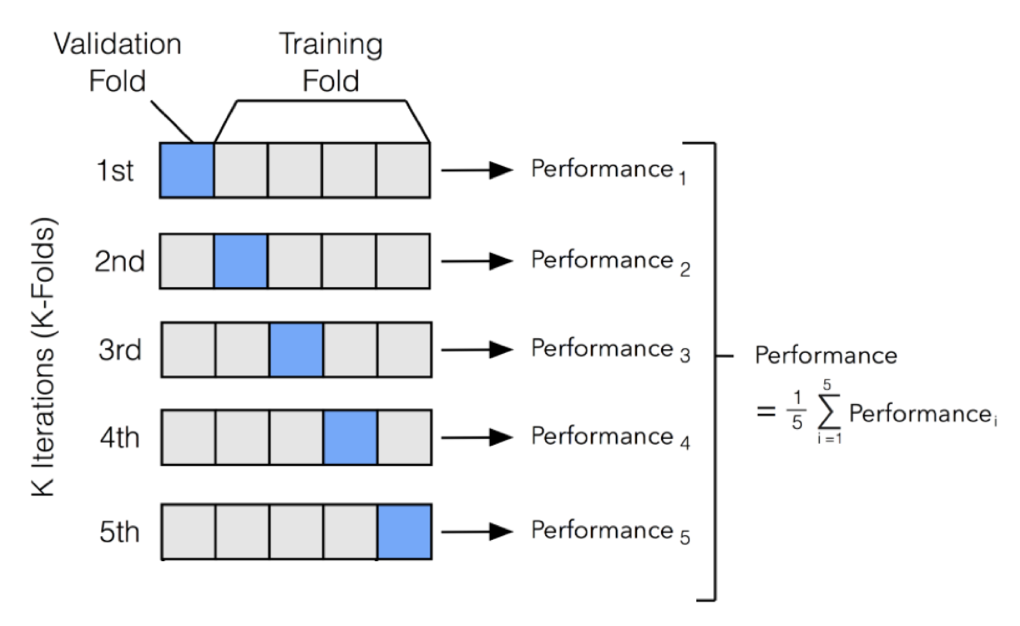
Regularization

Regularization은 회귀하고자 하는 선형 방정식을 간소화 하는 방식으로, 이는 neural network에서도 찾아볼 수 있다. 예를 들어 회귀한 선형방정식이 아래와 같을 때,

\[\begin{aligned} Y = \beta_0 + \beta_1X_1+\beta_2X_2^2+\beta_3X_1X_2 + \beta_4X_2^3 \end{aligned}\]

Lasso regularization은 $\beta_4= \beta_3=0$ 과 같이 일부 차원 (이 경우 $X_1X_2$와 $X_2^3$)의 효과를 없애는 식으로 과적합을 막는다. 하지만 이런 경우 몇 개의 중요한 차원만 남기는 식으로 오히려 모델의 부정확성이 커질 위험이 있기 때문에 Ridge regularization의 경우 확실히 0으로 만드는 Lasso 방식과 다르게 ‘0에 가까운($\beta_3\sim0,\beta_4\sim0$)’ 값으로 만든다. Open source scikit learn에서 load_boston 데이터에 대하여 Lasso와 Ridge 정규화를 적용했을 때 추정된 $\beta$에 해당하는 값들은 아래와 같다.

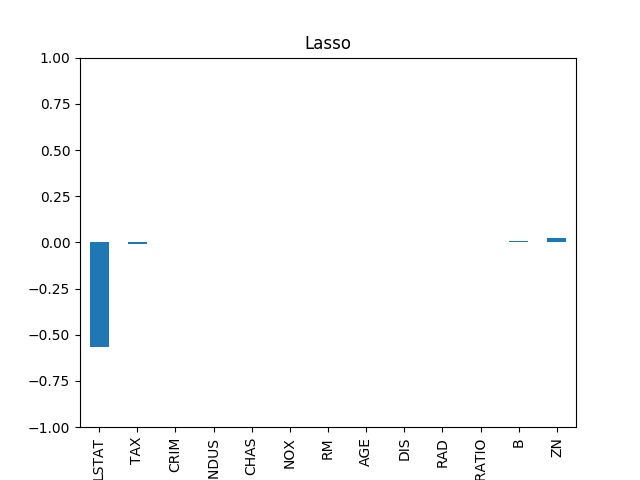Lasso Regression

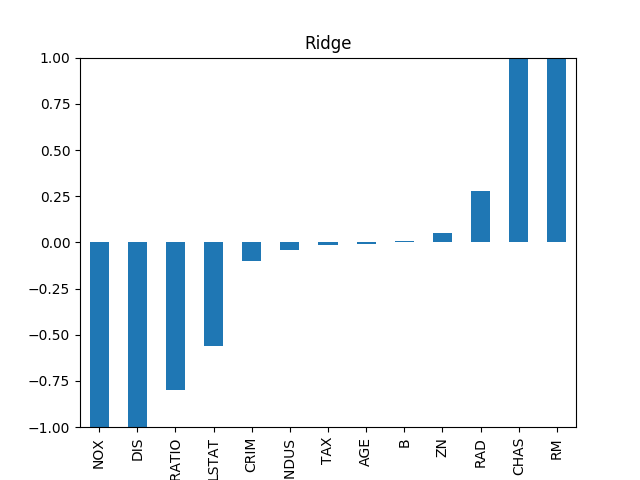Ridge Regression

특징점이 13개인 13차원의 데이터에 대하여 Lasso는 4개의 차원만 남기고 나머지 차원을 무시하도록 $\beta$ 값들이 추정되었고, Ridge의 경우 비율의 차이가 있을 뿐 모든 차원의 영향이 살아있도록 $\beta$ 값들이 추정된 것을 볼 수 있다.

두 가지 방식은 모델을 지나치게 단순하게 만들거나, 복잡성을 많이 줄이지 못하거나의 문제를 지니고 있다. 따라서 이 두가지 정규화 방식을 적당한 비율로 차용한 방식이 제안되었으며 이를 ElasticNet이라고 한다. 같은 데이터 셋에 대해 ElasticNet으로 \beta 값을 추정한 결과는 아래와 같다.

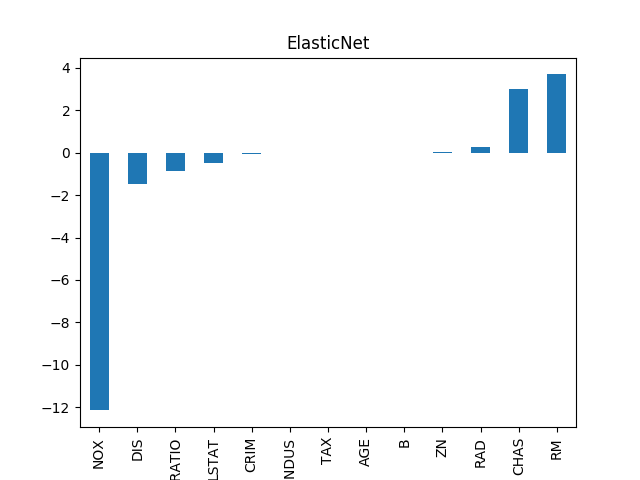ElasticNet Regression

Linear regression metric

회귀된 방정식을 통해 예측한 값에 대하여 성능은 $RSS$(Residual Sum of Squares), $MSE$(Mean Squared Error), $MAE$(Mean Absolute Error), $R^2$ 등의 지표로 파악한다.

• $RSS$: 오차의 제곱을 단순 합한 것으로, 오차의 크기에 의존적인 값으로 잘 사용되지 않음
• $MSE$: RSS를 데이터의 수 만큼 나눈 값으로 분산의 개념으로 볼 수 있다. 작을 수록 좋은 값이다.
• $MAE$: 오차의 절댓값을 데이터 수 만큼 나눈 값으로 MSE와 비슷하게 작을 수록 좋은 값이다.
• $R^2$: 1 - SSE(Sum of Squares Error)/SST(Sum of Squares Total)