Deep Learning Lecture2 - DeepLearning Techniques!

Learning with Various Optimizers

지난 포스트에서 설명했듯이, Multilayer Perceptron 기반 deep learning 방식은 다음과 같다.

1. 적당한 깊이의 multi layer perceptron을 설계한다. (weight 및 bias 초기화)
2. 주어진 input과 output에 대해 loss function을 계산한다.
3. gradient descent 방식을 사용해서 loss function을 최소화 하는 weight와 bias를 계산한다. (이 때 back propagation 사용)

하지만 loss function이 형태에 따라서 gradient descent 방식은 최소값을 구하는데 오랜 시간이 걸릴 수 있다는 문제가 있다. 왜냐하면, gradient descent 방식은 현재 지점의 변화량에 영향을 많이 받기 때문이다. 만약 global minimum point는 다른 곳에 있는데 local minium point 근처에 도달한 상태라면, 변화량 값 자체가 0에 가깝기 때문에 이를 벗어나는데 오랜 시간이 걸리게 된다.

이를 해결하기 위해서 gradient descent 방식에서 여러 가지 optimizer들이 파생되었고 (파생된 기법을 소개한 논문 인용수가 몇 만회는 된다.. ㄷㄷ) 종류에 대해서 간단히 소개하자면 아래와 같다.

SGD

Stochastic Gradient Descent 방식 optimizer로, 훈련 데이터를 여러 mini-batch 로 나누어서 각 mini batch에 대해 gradient descent를 수행하는 방식이다. 기존에 Gradient Descent 방식이 학습용 데이터의 갯수가 매우 클 때 불가피한 연산량 문제를 해결하기 위해 제안되었다.

지난 포스트에서 gradient descent가 훈련 데이터에 의해 생성된 loss function으로 만들어진 산 비탈길을 내려가는 방식이라고 했었다. SGD는 적은 이보다 적은 양의 훈련 데이터로 만든 loss function ‘유사 비탈길’이 모든 훈련 데이터로 만든 loss function 비탈길과 비슷하게 생길테니까, 이러한 ‘유사 비탈길’ 여러 개에 대해서 GD에서 했던 방식을 반복하자는 취지이다. SGD는 밑에서 소개되는 다양한 최적화 방식의 토대가 된다.

Momentum

Momentum 방식은 loss function의 local minimum을 빠져나오기 위해 생각할 수 있는 가장 기본적인 형태의 최적화 알고리즘이다. 산 비탈길을 따라 내려갈 때, 가파른 경사를 타고 내려가고 있었다면 그 관성을 이용하여 얕은 오르막을 탈출해서 local minimum을 벗어나자는 취지이다.

Adagrad

Adagrad 방식은 변화량이 작은 변수에 대해서 learning rate를 크게 하여 학습시켜야 할 모든 변수들의 속도를 비슷한 수준으로 맞추자는 취지의 알고리즘이다. learning rate는 산 비탈길을 내려갈 때 내딛는 보폭의 크기로 생각하면 편한데, 만약 산 비탈길과 같이 2D로 표현되는 지면에 대하여 Adagrad 방식을 적용한다고 하면 x축으로 정해진 보폭으로 움직였을 때 고도가 조금 작아진다고 하면, 고도 하강이 심한 y축에 대해서는 이에 맞추기 위해서 보폭을 좀더 낮춰서 내려가는 방식이다.

이렇게 하면 SGD보다 local minimum에 빠지는 위험을 줄일 수 있지만, 애초에 보폭을 줄여서 local minimum에 도달하는 위험을 피하자는 방식이기 때문에 학습이 진행될수록 점점 더 보폭이 작아져서 시간이 오래 걸린다는 단점이 있다.

RMSprop

RMSprop 방식은 이런 Adagrad의 방식을 보완하기 위해서 여태까지 줄여왔던 보폭의 크기를 잊어 버리는 방식을 사용했다. 공식적으로 publish된 방식은 아니지만, Adagrad에서 나타는 학습 지연 현상을 줄일 수 있게 되었다.

Adam

Adam은 RMSprop방식과 momentum 방식을 합한 것으로, 보통 deep learning을 할 때 제일 많이 쓰이는 최적화 방식이다.

여기서 소개된 방식 말고도 최적화 방식은 매우 많다. (여기를 참조) 여러 최적화 방식에 대해서 loss function 값이 줄어드는 속도는 아래 gif 파일을 통해서 확인해 볼 수 있다. 아래 그림을 확인해보자.

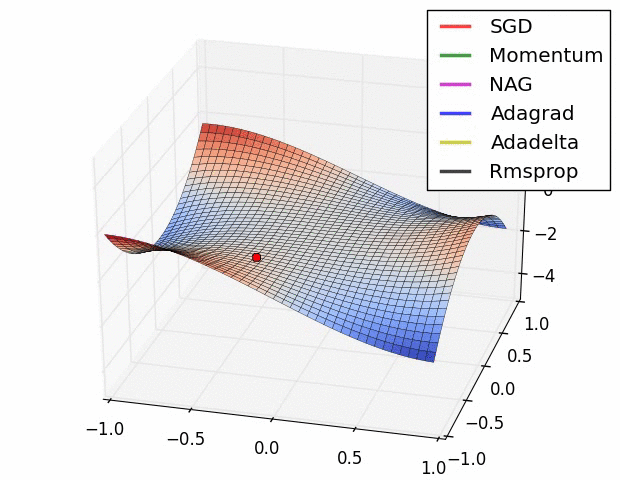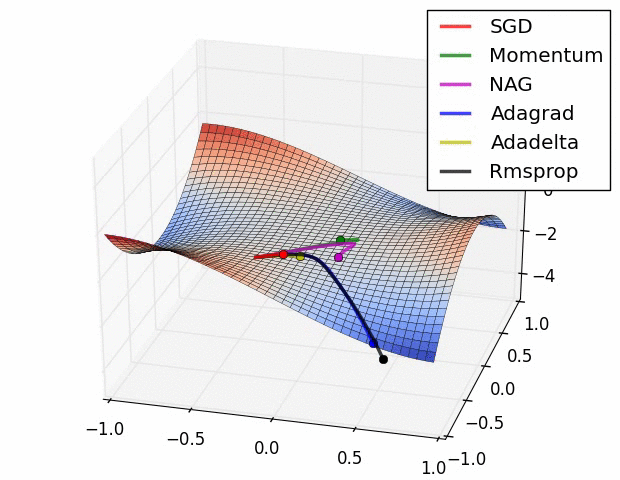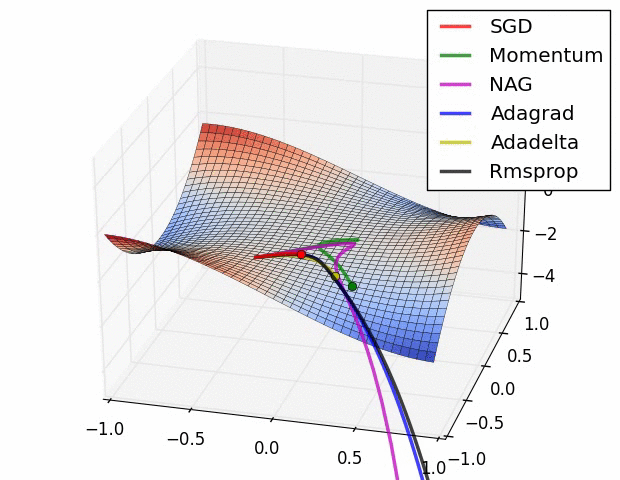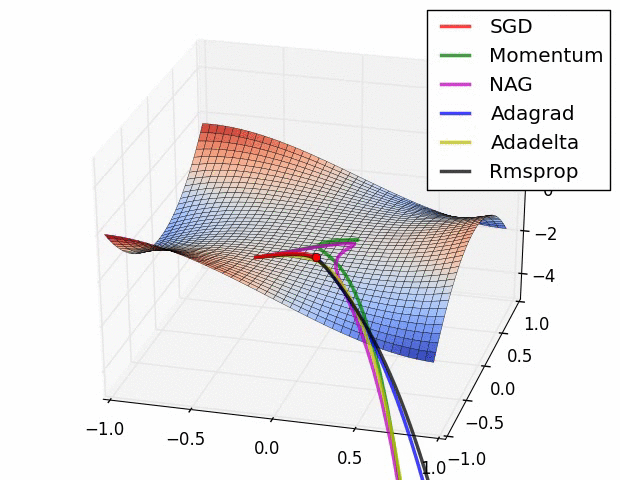
Prevent Overfitting

Layer를 최대한 많이 구성하고 각 layer에 넉넉하게 perceptron들을 채워서 학습을 시키면 어떠한 데이터에 데에서도 모델링을 할 수 있을 것 같지만, 그럴 경우 ‘학습에 사용한 데이터에만’ 잘 맞도록 설계된 모델링이 될 가능성이 있다.

이는 현실 세계에서도 찾아볼 수 있는 문제이다. 보통 대학생들은 자신의 전공 시험에 대비하기 위해 족보를 많이 풀어보곤 한다. 그러나 그 전공 시험 담당 교수가 작년 부로 은퇴를 하시고 새로 부임하신 열정 넘치는 교수님이 문제를 ‘직접’ 만들어냈다고 하자. 족보 문제에 ‘overfitting’된 학생들은 신임 교수가 낸 문제에 당황하여 제대로 된 점수를 받을 수 없을 것이다. 아래 그림을 확인해보자.

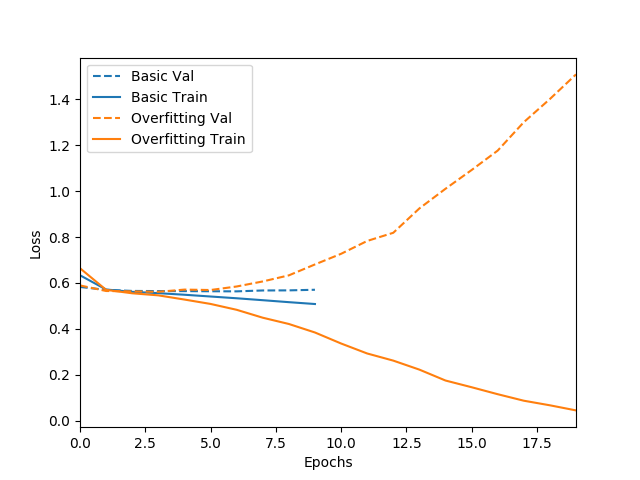
위 그림에서 파랑색 실선은 적당한 층의 layer와 적당한 수의 node로 구성된 model로 적당한 횟수만큼 학습을 시킨 결과로, 파랑색 점선을 보면 학습된 모델로 test용 데이터에 대해 결과 값을 예측할 때 대충 비슷한 양상으로 loss function이 내려가는 것을 확인할 수 있다.

그러나 노랑색의 경우 과한 깊이의 Layer와 과도한 수의 node로 구성된 model을 과한 횟수만큼 학습을 시킨 경우 훈련 데이터(실선)에 대해서는 loss function이 0에 가깝게 내려갈 정도로 overfitting 되었기 때문에 오히려 테스트용 데이터(점선)에 대해선 loss function이 증가하는 바람직하지 않은 결과가 나오게 됬다.

위의 예시 속 대학생이 만약 수업 때 교수가 강조한 포인트에 더 집중하고(Regularization) 족보 문제를 마지막 점검용으로 몇 개만(Dropout) 풀어봤다면, 더 좋은 점수를 받을 수 있을 것이다.

Regularization

학습시켜야 할 weight와 bias 중에서 의미 있는 것들만 남겨두고 나머지를 0(L1 Regularization), 또는 0에 가깝게(L2 Regularization) 남겨두는 방식을 Regularization이라고 한다.

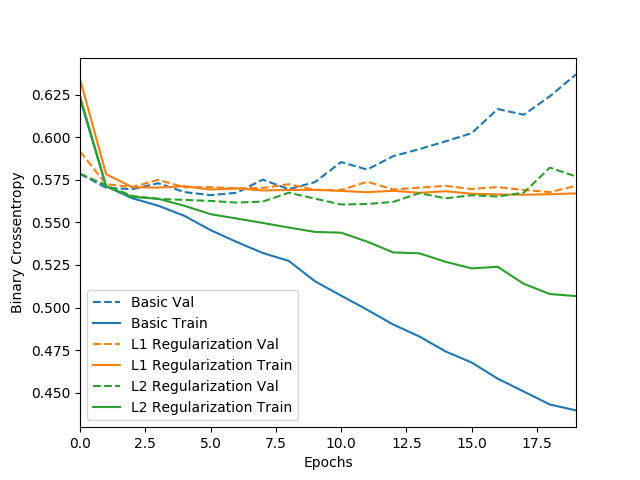
Regularization 방식을 사용하지 않은 파랑색 데이터의 경우 학습된 모델이 test용 데이터에 대해서 loss function이 증가하는 양상을 보이는 반면, 노랑색 및 초록섹 데이터는 의미 있는 weight만 남겨두어서 파랑색 데이터에 비해 학습된 모델이 test용 데이터에 대해서도 안정적으로 loss function을 줄이는 것을 볼 수 있다.

L2 Regularization (초록색)의 경우 학습된 모델이 L1 Regularization을 사용한 모델 (노랑색) 보다 train data에 대해서 overfitting이 일어나 loss function 값이 많이 줄어들었지만, test data에 대해서는 L1 Regularization을 사용한 방식과 유사한 loss function을 보이는 것을 알 수 있다. 따라서 L2 Regularization 방식은 상대적으로 overfitting 문제에 대해서 더 강인한 성능을 보여주는 것을 알 수 있다.

Dropout

학습시켜야 할 weight와 bias 중에서 확률적으로 일정 부분을 버리는 방식을 Dropout이라고 한다.

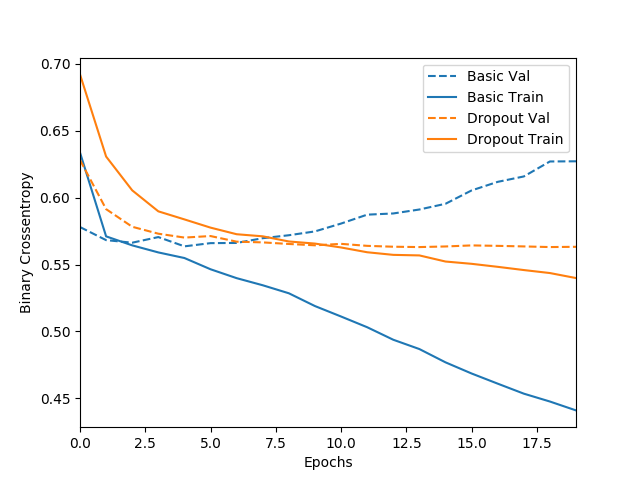
Dropout을 실시한 결과 그렇지 않았을 때에 비해 학습된 모델이 test data에 대한 loss function값이 train data에 대한 loss function값과 비슷한 것을 볼 수 있다. (overfitting되지 않고 적당히 학습됨)

How to Learn Faster?

위에서 설명한 일련의 방식들은 한 epoch (훈련용 데이터 전체에 대해서 한 번 학습 완료)에 대한 학습 속도를 여러 최적화 알고리즘 (SGD, Momentum, Adagrad, RMSprop, Adam, etc.)을 통해 개선하고, overfitting을 방지하는 방식들이었다.

하지만 비선형성이 매우 심한 시스템의 경우에는 여러 epoch을 걸쳐야만 학습이 완료되는 모델들도 있을 것이다. 그럴 경우에 사용되는 알고리즘이 batch normalization이라는 방식이다. normalization이라는 이름이 붙는 이유는 각 layer의 node들에 대입되는 input 값들에 대해서 normalization을 진행하기 때문이다. 최초 input 값들이 점점 더 깊은 layer에 도달하면서 어떤 layer에서는 input 값에 대해서 편중 현상이 심하게 일어날 수도 있기 때문에 수행하는 과정이다.

생각해보면 애초에 normalization은 최초 layer에 input 데이터를 입력시킬 때 수행하는 과정이었다. 예를 들어 학습시킬 때 input 데이터끼리 차원이 달라서 값의 범위가 매우 다른 경우를 보자. 키와 시력을 가지고 현역 1급 판정을 받을지 말지 예측하는 모델을 학습시킨다고 했을 때 키는 100이 넘어가는 수고 시력은 0~2 사이의 값이기 때문에 최초에 normalization을 수행하고 학습을 진행시킨다. Batch normalization은 그저 각 layer에 대해서 이런 normalization을 수행할 뿐이다. 아래 그림을 보자.

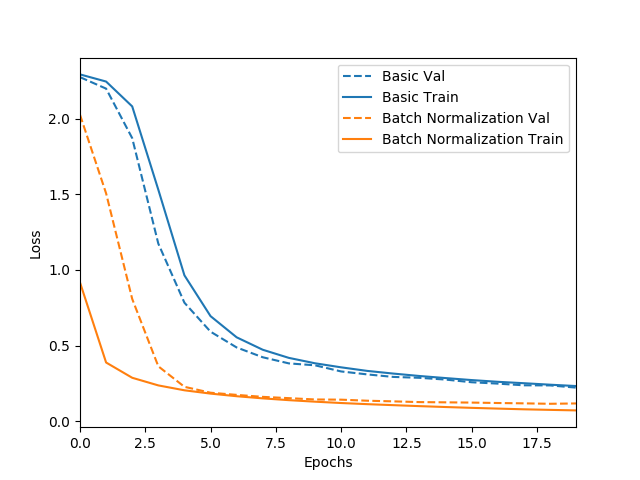
노랑색의 데이터가 batch normalization을 수행했을 때로, loss function이 0.2보다 작아졌을 때 학습을 마친다고 하면 batch normaliztion을 적용했을 때 10 epoch 이전에 학습이 완료되지만, 파랑색 데이터의 경우 학습을 훨씬 더 많이 진행해야 함을 알 수 있다.

batch normalization을 수행하는 경우 각 epoch 당 학습시간이 조금 더 늘어나긴 하지만, input 데이터의 차원이 매우 높아서 편중 현상이 일어나기 쉬운 모델일 수록 batch normalization 사용을 통해서 빠른 학습 결과를 기대해 볼 수 있다.