Deep Learning Lecture1 - How do Perceptrons Work?

Overview

Learn by Single Layer Perceptron

Perceptron은 뉴런을 모방한 모델로, 뉴런처럼 행동하기 때문에 구조도 간단하다. 그저 input 신호에 대해서 weight를 곱하고 bias를 더한 신호에 activation function (sigmoid, relu, tanh 등)을 통과시킨 값을 output으로 하는 구조일 뿐이다.

이 단일 Perceptron 하나로 뭘 할 수 있을까? 어떤 탐욕스런 개발자가 주식으로 떼돈을 벌기 위해서 전날 나스닥의 등락 포인트(input)가 주어졌을 때 다음날 코스피의 등락 포인트(output)를 5년동안 기록한 데이터가 있다고 하자. 매일같이 기록한다고 했을 때, 5 x 365 = 1825개의 (input, output) 쌍을 가지고 있을 것이다.

만일 이 perceptron의 weight 와 bias가 어떤 수로 결정되었을 때 개발자가 기록한 input을 대입시켜 봤더니 여태 기록한 output과 기가막히게 일치한다면, 이 개발자는 앞으로 이 perceptron에 나스닥 등락포인트만 넣는다면 일할 필요 없이 돈을 벌 수 있게 된다.

문제는 weight랑 bias가 어떤 수가 될지 결정해야 한다는 것이다. 다행히 개발자는 ‘기계 학습’을 공부한 적이 있어 자신이 시행착오를 겪으며 1825번의 계산을 하지 않았다. 개발자는 초기값이 적당히 세팅된 perceptron이 뱉어낸 1825개의 예측값에 자신이 기록한 1825개의 값을 빼서 얻은 1825개의 오차 값을 합해서 이를 ‘손실 함수(loss function)’으로 정했다. 그리고 대학교 때 배운 미분을 사용해서 손실 함수 값을 최소로 하는 weight와 bias값을 구했다.

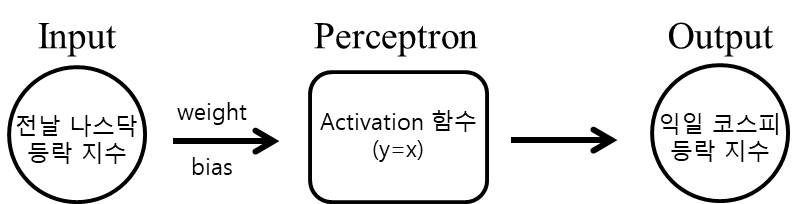
위의 과정이 (input, output)이 주어질 때 최적의 perceptron을 구하는 과정의 전부다. 사실 주가를 결정하는 요인은 한 두개가 아니라서 위 개발자는 자신이 얻은 perceptron에 의존하다가는 망하겠지만(선형대수를 알고 눈치가 좀 빠른 사람이라면 위와 같은 activation function을 가지는 단일 perceptron의 구조가 선형(linear)이라는 것을 파악할 수 있다. 즉, output = input * weight + bias 구조이므로, 그냥 least squares 방식으로 구하면 끝이다.), AND, OR, NOR 과 같이 단순한 형태의 게이트는 위의 방식으로 구현할 수 있다.

AND 게이트의 경우 input이 둘 다 참(1)이어야 output이 참(1)이므로, 추정해야할 wieght는 두 개, bias도 두 개로 총 4개의 미지수를 추정해야 한다. 각 weight가 0.5, bias가 -0.3로 설정된다면 AND 게이트가 완성된다.

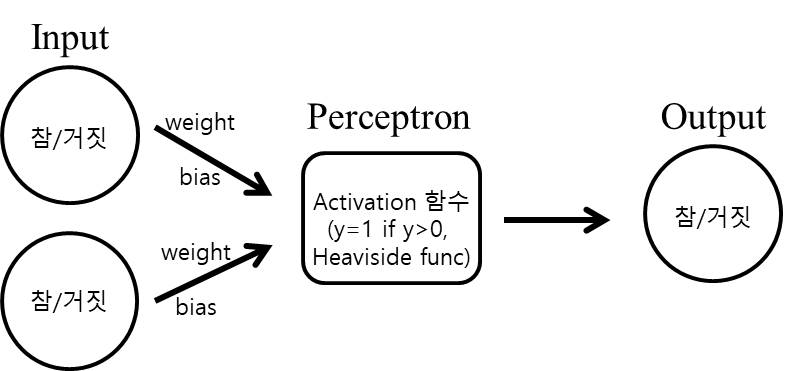
Learn by Multi Layer Perceptron

하지만 단일 perceptron은 비선형 함수의 표현에 한계가 있다. 단순하게 XOR 게이트를 구현하는 경우만 봐도 단일 perceptron으로는 구현이 불가능 한 것으로 알려져 있다. (아래의 그림과 같이)

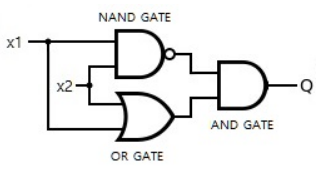
이렇게 input과 output 사이에 존재하는 perceptron 층을 hidden layer라고 부르고, 이러한 hidden layer가 많아질 수록 비선형성이 높은 함수를 표현할 수 있게 된다. (대신에 hidden layer를 구성하는 perceptron 갯수 만큼 학습시켜야 할 weight와 bias가 많아질 것이다.)

weight와 bias의 학습은 위에서 들은 ‘주식 모델을 학습시킨 개발자’ 예시에서 말한 것 처럼 loss function이 최소가 될 때까지 진행해시켜야 한다. loss function은 multilayer을 구성하는 weight와 bias 값에 따라 값이 결정되니까, 우리는 loss function을 최소로 하는 weight와 bias를 찾으면 된다.

weight와 bias를 찾는 방식은 ‘Gradient Descent’ 방식을 사용하는 것이다. 이는 맹인이 산 정상을 내려가는 원리로, 자신이 서 있는 지점에서 경사가 가장 가파르다고 생각하는 곳을 따라 내려가는 것이다. 맹인 입장에서는 횡축, 종축으로 표현된 2차원 지면에 대해서 어느방향을 가야 제일 비탈질 지 고려하면 되지만, 우리가 설계한 loss function은 perceptron들을 표현하는 수 많은 weight와 bias로 이루져 있다. (고차원)

ref:TowordDataScience

multi layer perceptron의 경우 bias와 weight가 input layer 쪽에 있을 수록 각 변화가 안 쪽에 있는 hidden layer에 의해 영향을 받게 된다. 따라서 어떤 weight, bias들의 변화량이 loss function의 변화량에 어떤 영향을 미칠지는 다른 weight와 bias들도 고려해야 하는데, 이를 고려한 방식이 back propagation 이다. (back propagation에 대한 자세한 설명은 graph computation 이론을 사용해서 설명한 스탠포드 강의를 참고하면 좋다.) 방식이 어려울 것 같지만 핵심은 편미분 값을 chain rule에 의해 구하는 것 뿐으로, 그 원리는 아래의 그림과 같다.

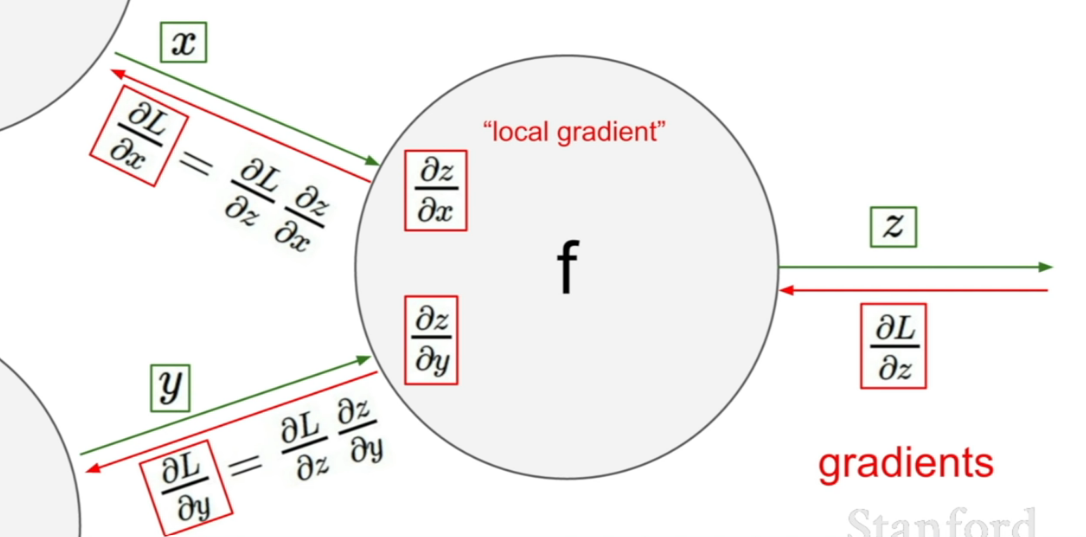ref:Youtube:Standford University School of Enginnering

결론적으로, multi layer perceptron 기반 딥러닝의 단계는 다음과 같다.

1. 적당한 깊이의 multi layer perceptron을 설계한다. (weight 및 bias 초기화)
2. 주어진 input과 output에 대해 loss function을 계산한다.
3. gradient descent 방식을 사용해서 loss function을 최소화 하는 weight와 bias를 계산한다. (이 때 back propagation 사용)