칼만필터 유도 - 2. Minimum variance based method

본 포스트의 내용은 Simon, Dan. Optimal state estimation: Kalman, H infinity, and nonlinear approaches. John Wiley & Sons, 2006. 저서에 기반하고 있습니다.

측정치가 주어진 확률 모델이 maximum likelihood를 가지도록 하는 추정치를 유도한 지난 포스트와는 다르게, 이번 시간에는 추정 오차의 공분산을 최소화 하는 방식인 minimum variance based method로 칼만필터를 유도해보겠습니다.

1. Modeling

유도하는 방식만 다를 뿐, 모델링은 아래 그림처럼 maximum likelihood based method에서 사용한 시스템을 그대로 사용합니다.

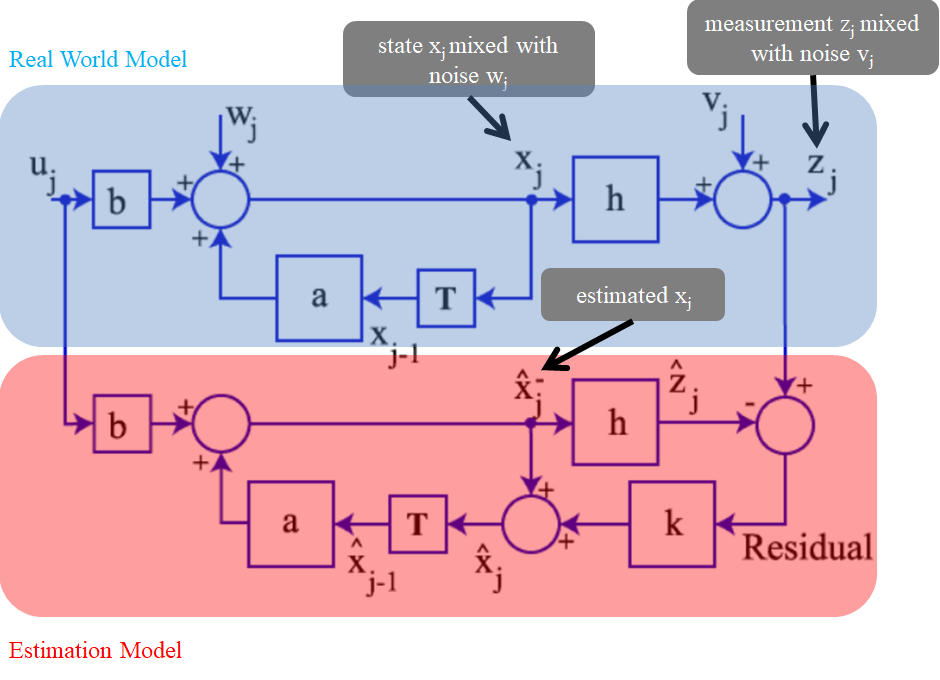Reference:link

즉, $E[\mathbf{\hat{x}}_k]=\mathbf{\bar{x}}_k$ 라는 unbiased estimator 가정을 따르는 estimation model에서 real world model의 측정치 $\mathbf{z}_k$ 를 사용해서 추정을 진행하는 것입니다.

주어진 블록 다이어그램에 의해 측정치 $\mathbf{z}_k$ 에 의한 업데이트를 진행하는데 필요한 식은 아래와 같습니다. 칼만필터에 대한 모델링 과정이 왜 위의 블록 다이어 그램처럼 유도가 되는 지 궁금하시다면 maximum likelihood based 방식으로 칼만필터를 유도한 지난 포스트 를 참고하면 좋을 것 같습니다.

\[\begin{align} \mathbf{z}_k &= \mathbf{H}_k\mathbf{x}_k+\mathbf{v}_k\\ \mathbf{\hat{x}}_k^+ &= \mathbf{\hat{x}}_{k}^- + \mathbf{K}_k(\mathbf{z}_k-\mathbf{H}_k\mathbf{\hat{x}}_{k}^-)\tag{1} \end{align}\]

2. Problem statement

이번에는 추정 오차의 공분산 값을 최소화 하는 방식으로 칼만필터를 유도해보겠습니다. Random vector $\mathbf{x}_k\in \mathbb{R}^n$ 을 추정시, n 개의 element ($\mathbf{x}^1_k,\mathbf{x}^2_k,\cdots,\mathbf{x}^n_k$) 에 대하여 추정오차 $\mathbf{e}_k^i=\mathbf{x}_k^i-{\mathbf{\hat{x}}_k^i}^+$가 존재합니다. 따라서 모든 element의 추정 오차 공분산의 합을 최소화 하는 추정치 $\mathbf{\hat{x}}$ 를 구하도록 칼만필터를 유도해 보겠습니다. 최소화 해야하는 값 $J_k$ 는 다음과 같이 나타낼 수 있습니다.

\[\begin{align} J_k &= E[(\mathbf{x}_k^1-\mathbf{\hat{x}}_k^1)^2] + \cdots + E[(\mathbf{x}_k^n-\mathbf{\hat{x}}_k^n)^2]\\ &=E[\epsilon_{x1,k}^2+\cdots+\epsilon_{xn,k}^2]\\ &=E[\epsilon_{x,k}^T\epsilon_{x,k}]\\ &=E[Tr(\epsilon_{x,k}\epsilon_{x,k}^T)]\\ &=Tr(\mathbf{P}_k)\tag{2} \end{align}\]

3. Derivation

3-1. Estimation error covariance P

식 (1)을 이용한 추정오차의 공분산은 다음과 같습니다.

\[\begin{aligned} \mathbf{P}_k &= E[\epsilon_{x,k}\epsilon_{x,k}^T]\\ &= E{[\mathbf{I}-\mathbf{K}_k\mathbf{H}_k][\cdots]^T}\\ &= (\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)E[\epsilon_{x,k-1}\epsilon_{x,k-1}^T](\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)^T-\\ &\quad\,\,\mathbf{K}_kE[v_k\epsilon_{x,k-1}^T](\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)^T-(\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)E[\epsilon_{x,k-1}v_k^T]\mathbf{K}_k^T+\\ &\quad\,\,\mathbf{K}_kE[v_kv_k^T]\mathbf{K}_k^T \end{aligned}\]

여기서 k-1의 시점에서 추정오차와 k 시점에서 측정치의 noise는 서로 independent 하기 때문에, 다음이 성립합니다.

\[\begin{aligned} E[v_k\epsilon_{x,k-1}^T]&=E[v_k]E[\epsilon_{x,k-1}]=0 \end{aligned}\]

따라서

\[\begin{align} \mathbf{P}_k = (\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)\mathbf{P}_{k-1}(\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)^T+\mathbf{K}_k\mathbf{R}_k\mathbf{K}_k^T\tag{3} \end{align}\]

3-2. Kalman gain $\mathbf{K}$

한편, 식 (2)에서 $Tr(\mathbf{P}_k)$ 를 최소화 하는 $\mathbf{K}_k$ 는 $\frac{\partial{J_k}}{\partial{\mathbf{K}_k}}=0$ 이 되는 지점을 찾는 것으로 구할 수 있습니다. 행렬에 Trace가 적용될 때의 편미분에 관련해서는 [여기]를 참고하기 바랍니다.

\[\begin{aligned} \frac{\partial{J_k}}{\partial{\mathbf{K}_k}}=2(\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)\mathbf{P}_k(-\mathbf{H}_k^T)+2\mathbf{K}_k\mathbf{R}_k=0 \end{aligned}\]

그러므로,

\[\begin{aligned} \mathbf{K}_k\mathbf{R}_k&=(\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)\mathbf{P}_{k-1}\mathbf{H}_k^T\\ \mathbf{K}_k(\mathbf{R}_k+\mathbf{H}_k\mathbf{P}_{k-1}\mathbf{H}_k^T)&=\mathbf{P}_{k-1}\mathbf{H}_k^T\\ \mathbf{K}_k&=\mathbf{P}_{k-1}\mathbf{H}_k^T(\mathbf{H}_k\mathbf{P}_{k-1}\mathbf{H}_k^T+\mathbf{R}_k)^{-1} \end{aligned}\tag{4}\]

4. Conclusion

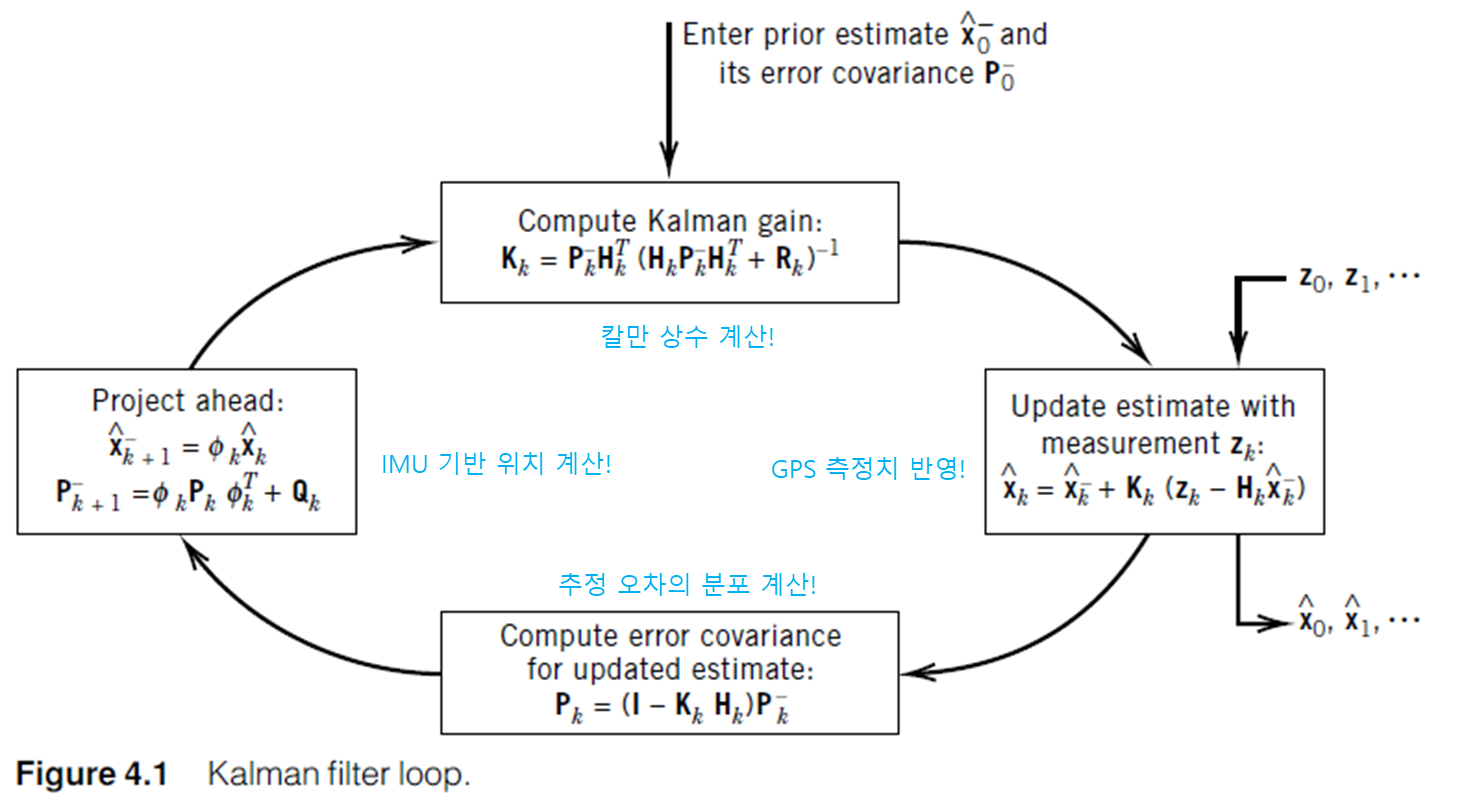
유도된 결과는 다음과 같습니다.

\[\begin{aligned} \mathbf{K}_k&=\mathbf{P}_{k-1}\mathbf{H}_k^T(\mathbf{H}_k\mathbf{P}_{k-1}\mathbf{H}_k^T+\mathbf{R}_k)^{-1}\\ \mathbf{\hat{x}}_k&=\mathbf{\hat{x}}_{k-1}+\mathbf{K}_k(\mathbf{z}_k-\mathbf{H}_k\mathbf{\hat{x}}_{k-1})\\ \mathbf{P}_k&=(\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)\mathbf{P}_{k-1}(\mathbf{I}-\mathbf{K}_k\mathbf{H}_k)^T+\mathbf{K}_k\mathbf{R}_k\mathbf{K}_k^T \end{aligned}\]