칼만필터 유도 - 1. Maximum likelihood based method

지난 포스트의 4. 결론 부분에서 posterior density는 측정치가 반영된 확률 모델이 가지는 추정치에 대한 likelihood라고 했습니다. 그리고 이 likelihood를 최대화 하는 과정에서 kalman filter가 유도 된다고 했습니다. 이번 시간에는 maximum likelihood를 가지도록 하는 추정치를 구하면서 kalman filter를 유도해보겠습니다. 유도 과정에서 식이 좀 많이 필요하며, 보통 전공책에서는 tedious 또는 laborious 한 유도과정이라고 생략되어 있는 경우가 많습니다. (실제로 해보면 매우 tedious 하고 laborious 하기도 합니다$\dots$)

1. Problem Statement

State $\mathbf{x}_k$ 에 대해서 측정치 $\mathbf{z}_k$ 가 반영된 확률 모델이 가지는 likelihood, 그러니까 $p(\mathbf{x}_k|\mathbf{z}_k)$ 가 최대값을 가지도록 하는 최적화 문제를 풀어야 합니다. 편의상 시점에 관한 아래 첨자는 생략하도록 하겠습니다. Bayes rule에 의하여 likelihood를 $\mathbf{x}$ 에 대해서 나타낼 수 있으므로 결국 $\underset{\mathbf{x}}{\operatorname{argmax}}$ $p(\mathbf{x}|\mathbf{z})$ 를 구하면 됩니다.

2. Modeling

먼저, random vector $\mathbf{x}$ 와 measurement vector $\mathbf{z}$ 에 대하여 다음과 같은 모델을 따른다고 가정합니다. (vector와 matrix의 경우 scalar값과 구분하기 위해서 볼드체 사용)

\[\mathbf{x}=\mathbf{ax+bu+w}\\ \mathbf{z}=\mathbf{Hx+v}\]

여기서 $\mathbf{w}\sim N(\mathbf{0},\mathbf{Q})$, $\mathbf{v}\sim N(\mathbf{0},\mathbf{R})$, $E[\mathbf{x}\mathbf{v}^T]=\mathbf{0}$, $E[\mathbf{w}\mathbf{v}^T]=\mathbf{0}$ 으로, process 및 measurement noise는 평균이 0이고 각각 공분산이 $\mathbf{Q}$, $\mathbf{R}$ 인 정규분포를 따르는 white noise 이며 $\mathbf{x}$ 와 measurement noise 간, 그리고 process noise와 measurement noise 간의 cross correlation은 없다고 가정합니다. 한편, 입력 $\mathbf{u}=0$인 경우 random vector $\mathbf{x}\in \mathbb{R}^n$에 대하여 Gaussian distribution의 probability density function(pdf)는 다음과 같이 표현됩니다.

\[p(\mathbf{x})=\frac{1}{(2\pi)^{n/2}|\mathbf{Q}|^{1/2}}exp\biggl[-\frac{1}{2}(\mathbf{x-\bar{x}})^T\mathbf{Q}^{-1}(\mathbf{x-\bar{x}})\biggr]\]

한편, Bayes rule에 의해서 다음이 성립합니다.

\[p(\mathbf{x|z})=\frac{p(\mathbf{z|x})p(\mathbf{x})}{p(\mathbf{z})}\]

따라서 1. Problem Statement에서 식은 다음과 같이 전개 됩니다. (앞에 곱해진 상수 값은 최대, 최소값을 구하는 과정에 있어서 무시 가능)

\[\begin{align} &\quad\:\underset{\mathbf{x}}{\operatorname{argmax}}\text{ }p(\mathbf{x}|\mathbf{z})\\ &=\underset{\mathbf{x}}{\operatorname{argmax}}\text{ }exp\biggl[ -\frac{1}{2}(\mathbf{z-Hx})^T\mathbf{R}^{-1}(\mathbf{z-Hx}) -\frac{1}{2}(\mathbf{x-\bar{x}})^T\mathbf{Q}^{-1}(\mathbf{x-\bar{x}}) +\frac{1}{2}(\mathbf{z-H\bar{x}})^T(\mathbf{HQH}^T+\mathbf{R})^{-1}(\mathbf{z-H\bar{x}}) \biggr]\tag{1} \end{align}\]

이렇게 전개 되는 이유는 다음이 성립하기 때문입니다.

\[\begin{aligned} E[\mathbf{z}]&=E[\mathbf{Hx+v}]=\mathbf{H\bar{x}}\\ Var\text{ }\mathbf{z} &=E[(\mathbf{z-\bar{z}})(\cdots)^T]\\ &=E[(\mathbf{Hx+v-H\bar{x}})(\cdots)^T]\\ &=E[(\mathbf{H(x-\bar{x}})+\mathbf{v})(\cdots)^T]\\ &=\mathbf{H}E[(\mathbf{x-\bar{x}})(\mathbf{x-\bar{x}})^T]\mathbf{H}^T+E[\mathbf{vv}^T]\\ &=\mathbf{HQH}^T+\mathbf{R}\\ \end{aligned}\]

식 (1)에서 마지막 항은 x에 대한 식이 아닌 상수 값이므로 최댓값을 구하는 과정에서 제외할 수 있는 항이고, 남은 항에 대해서 쓰게 되면 결국 문제는 다음과 같이 바뀌게 됩니다.

\[\underset{\mathbf{x}}{\operatorname{argmin}}\text{ }J\] \[\begin{aligned} where\text{ }J&=\frac{1}{2}(\mathbf{z-Hx})^T\mathbf{R}^{-1}(\mathbf{z-Hx}) +\frac{1}{2}(\mathbf{x-\bar{x}})^T\mathbf{Q}^{-1}(\mathbf{x-\bar{x}}) \end{aligned}\]

3. Derivation

3-1. Deriving estimated state $\hat{x}$

이제 남은 일은 J를 $\mathbf{x}$ 에 대해서 미분한 뒤, 이 때 값이 0이 되는 x를 찾으면 됩니다. 더욱더 확실하게 하려면 $\mathbf{x}$ 에 대해서 두 번 미분한 값이 항상 양의 값을 가지는지 따져야 미분해서 0이 되는 지점이 최솟값이 되는지를 확신할 수 있지만, 너무 길어지는 관계로 그 과정은 생략하겠습니다.

현재 $J$ 는 scalar 값 이지만, 벡터 $\mathbf{x}$ 에 대해 미분해야 합니다. 스칼라의 벡터에 대한 미분은 [여기]를 참고하면 됩니다. 스칼라의 벡터 미분 방법에 따라 $\frac{\partial{J}}{\partial{\mathbf{x}}}$ 를 전개하면

\[\begin{aligned} \frac{\partial{J}}{\partial{\mathbf{x}}} &=\frac{1}{2}(\mathbf{-H})^T\mathbf{R}^{-1}(\mathbf{z-Hx}) +\frac{1}{2}\biggl[(\mathbf{z-Hx})^T\mathbf{R}^{-1}(\mathbf{-H})\biggr]^T +\frac{1}{2}(\mathbf{Q}^{-1})(\mathbf{x-\bar{x}}) +\frac{1}{2}[(\mathbf{x-\bar{x}})^T(\mathbf{Q}^{-1})]^T\\ &=\frac{1}{2}\{\mathbf{-H}^T\mathbf{R}^{-1}(\mathbf{z-Hx})+(\mathbf{Q}^{-1})(\mathbf{x-\bar{x}})\} \end{aligned}\]

따라서 $\mathbf{H}^T\mathbf{R}^{-1}(\mathbf{z-Hx})=(\mathbf{Q}^{-1})(\mathbf{x-\bar{x}})$ 를 만족할 때 x 값이 maximum likelihood값을 가지도록 하는 값입니다. 이제 x에 대해서 식을 다시 정리하면

\[\mathbf{H}^T\mathbf{R}^{-1}\mathbf{z}-\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H}\mathbf{x}=\mathbf{Q}^{-1}\mathbf{x}-\mathbf{Q}^{-1}\mathbf{\bar{x}}\]

$\mathbf{x}$에 대하여 식을 이항하면

\[\begin{aligned} &(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})\mathbf{x}\\ &=\mathbf{Q}^{-1}\mathbf{\bar{x}}-\mathbf{H}^{T}\mathbf{R}^{-1}\mathbf{z}\\ &=\mathbf{Q}^{-1}\mathbf{\bar{x}}+(\mathbf{H}^{T}\mathbf{R}^{-1}\mathbf{H}-\mathbf{H}^{T}\mathbf{R}^{-1}\mathbf{H})\mathbf{\bar{x}}+\mathbf{H}^{T}\mathbf{R}^{-1}\mathbf{z}\\ &=(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})\mathbf{\bar{x}}+\mathbf{H}^{T}\mathbf{R}^{-1}(\mathbf{z}-\mathbf{H\bar{x}}) \end{aligned}\]

이 때 나오는 $x$ 값을 추정치 $\hat{x}$ 라고 하면,

\[\begin{align} \therefore \mathbf{\hat{x}}=\mathbf{\bar{x}}+(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}(\mathbf{z}-\mathbf{H\bar{x}})\tag{2} \end{align}\]

3-2. Deriving estimation error covariance $\mathbf{P}$

State $\mathbf{x}$ 에 대해서 유도된 추정치의 $\mathbf{\hat{x}}$ 의 정확도는 두 값의 차이인 $\mathbf{x}-\mathbf{\hat{x}}$ 의 분포를 분석해서 나타날 수 있습니다. 이 값을 estimation error라 하고 (편하게 error, $\mathbf{e}$), 분포를 분석하기 위해 평균과 공분산값을 유도하겠습니다. 먼저 error의 평균 $E[\mathbf{e}]$ 는 식 (2)에 평균을 취해서 구할 수 있습니다.

\[\begin{aligned} E[\mathbf{e}]&=E[\mathbf{x}-\mathbf{\hat{x}}]\\ &=\mathbf{\bar{x}}-E[\mathbf{\hat{x}}]\\ &=-(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}(E[\mathbf{z}]-\mathbf{H\bar{x}})\\ &=0 \end{aligned}\]

따라서 error의 평균은 0인 것을 볼 수 있습니다. 바꿔말해 $E[\mathbf{x}-\mathbf{\hat{x}}]=0$ 이 성립하므로 $E[\mathbf{\hat{x}}]=\mathbf{\bar{x}}$ 입니다. 이렇게 state $\mathbf{x}$ 가 가지는 분포와 $\mathbf{\hat{x}}$ 가 가지는 분포에 대해서 두 분포의 평균값이 일치하는 결과가 나왔기 때문에 bias가 없는 추정치라고 표현합니다. (unbiased estimator)

이번에는 error의 공분산 값을 살펴보겠습니다.

\[\begin{align} &E[(\mathbf{e}-\mathbf{\bar{e}})(\mathbf{e}-\mathbf{\bar{e}})^T]\\ &=E[(\mathbf-\mathbf{\hat{x}})(\mathbf-\mathbf{\hat{x}})^T]\\ &=E[\{\mathbf{x}-(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}(\mathbf{z}-\mathbf{H\bar{x}})\}\{\cdots\}^T]\tag{3} \end{align}\]

여기서 편의를 위해 $(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}$ 대신 상수 $\mathbf{C}$ 를 사용하겠습니다.

\[\begin{aligned} &=E[\{\mathbf{x}-\mathbf{C}(\mathbf{H}(\mathbf{x-\bar{x}})+\mathbf{v})\}\{\cdots\}^T]\\ &=E[\{(\mathbf{I-CH})(\mathbf{x-\bar{x}})-\mathbf{Cv}\}\{\cdots\}^T]\\ &=E[\{(\mathbf{I-CH})(\mathbf{x-\bar{x}})(\mathbf{I-CH})(\mathbf{x-\bar{x}})\}]+E[\mathbf{Cvv^TC^T}]\\ &-E[\{(\mathbf{I-CH})(\mathbf{x-\bar{x}})\mathbf{v}^T\mathbf{C}\}]-E[\{\mathbf{C}\mathbf{v}(\mathbf{x-\bar{x}})^T(\mathbf{I-CH})\}]\\ \end{aligned}\]

여기서 state $\mathbf{x}$ 와 measurement noise $\mathbf{v}$ 간에 correlation은 없으므로 마지막 두 항은 0에 해당합니다. 따라서 추정오차의 공분산 $\mathbf{P}$ 는

\[\mathbf{P}=(\mathbf{I-CH})\mathbf{Q}(\mathbf{I-CH})^T+\mathbf{CRC}^T\tag{4}\]

아직 $\mathbf{C}$ 에 대한 식이 대입되지 않았습니다. 여기서 추가작업을 더 해주면 긴 형태의 $\mathbf{C}$ 를 더 간단하게 나타낼 수 있습니다. $\mathbf{C}$ 의 앞부분에 해당하는 부분을 $\mathbf{B}$ 라고 하면, 즉, $\mathbf{B}=(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}$ 일 때,

\[\begin{align} \mathbf{C}=\mathbf{BH}^T\mathbf{R}^{-1}\tag{5} \end{align}\]

또한,

\[\begin{aligned} \mathbf{B}^{-1}&=\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H}\\ \mathbf{I}&=\mathbf{BQ}^{-1}+\mathbf{BH}^T\mathbf{R}^{-1}\mathbf{H}\\ &=\mathbf{BQ}^{-1}+\mathbf{CH} \end{aligned}\] \[\therefore\mathbf{I-CH}=\mathbf{BQ}^{-1}\tag{6}\]

(5)와 (6)을 (4)에 대입하면,

\[\begin{align} \mathbf{P}&=\mathbf{BQ}^{-1}\mathbf{Q}(\mathbf{BQ^{-1}})^T+\mathbf{BH}^T\mathbf{R}^{-1}\mathbf{RR}^{-1}\mathbf{HB}^T\\ &=\mathbf{BQ}^{-1}\mathbf{B}^T+\mathbf{BH}^T\mathbf{R}^{-1}\mathbf{HB}^T\\ &=\mathbf{B}(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})\mathbf{B}^T\\ &=\mathbf{BB}^{-1}\mathbf{B}^T\\ &=\mathbf{B} (\because \mathbf{B}^T=\mathbf{B})\\ &=(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\tag{7} \end{align}\]

따라서 오차 공분산 $\mathbf{P}$ 는 $(\mathbf{I-CH})\mathbf{Q}(\mathbf{I-CH})^T+\mathbf{CRC}^T$ 이나 $(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}$ 로 나타낼 수 있고, $\mathbf{B}=\mathbf{P}$ 이므로 식 (5)는 $\mathbf{C}=\mathbf{PH}^T\mathbf{R}^{-1}$ 로 나타낼 수 있게 됩니다.

4. Validation

4-1. Replace $\mathbf{\bar{x}}$ with $\mathbf{\hat{x}}$

다시 시점을 아래첨자에 표시하여 유도한 결과를 정리하면 다음과 같습니다.

\[\begin{align} \mathbf{\hat{x}}_k&=\mathbf{\bar{x}}_k+\mathbf{C}(\mathbf{z}_k-\mathbf{H\bar{x}}_k)\tag{8}\\ \end{align}\] \[\begin{align} \mathbf{P}=(\mathbf{Q}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1} &=(\mathbf{I-CH})\mathbf{Q}(\mathbf{I-CH})^T+\mathbf{CRC}^T\tag{9} \end{align}\]

다 유도된 것처럼 보이지만, 식 (8)을 유심히 보면 뭔가 미심쩍은게 있습니다. 그건 바로 시점 k에서 추정치를 구하는데, 추정 대상인 state $\mathbf{x}_k$ 의 평균값 $\mathbf{\bar{x}}_k$ 을 사용한다는 것입니다. 추정치를 구하기 위해 참값을 사용한다..? 이는 불가능하므로, 그렇기 때문에 $\mathbf{\bar{x}}_k$ 대신 실시간 추정 결과인 $\mathbf{\hat{x}}_k$ 를 사용하기로 합니다.

비록 $\mathbf{\bar{x}}_k$ 는 deterministic 한 값이고 $\mathbf{\hat{x}}_k$ 는 평균과 공분산에 의한 분포를 가지는 stochastic한 값이지만 괜찮습니다. 3-2. 에서 유도한 것 처럼 추정치의 평균은 $\mathbf{\bar{x}}_k$ 가 되는 **unbiased estimator**이기 때문에 평균적으로는 $\mathbf{\hat{x}}_k$ 가 $\mathbf{\bar{x}}_k$ 처럼 행동할 것이고, 오차 공분산이 작으면 작을수록 더욱 $\mathbf{\bar{x}}_k$ 처럼 행동할 것이기 때문입니다.

$\mathbf{\bar{x}}_k$ 가 따르는 모델(2. Modelling에 평균을 취해서 noise항이 0으로 감)을 $\mathbf{\hat{x}}_k$ 도 따른다고 가정하고 (물론 처음에는 모델링 에러가 발생할 것입니다.), block diagram을 그려 봅시다. 먼저 원래의 모델은 아래 그림처럼 표현됩니다.

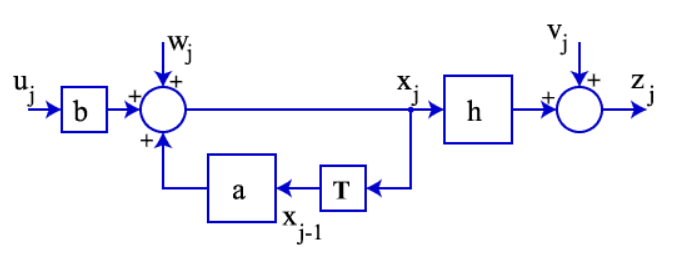출처:link

$\mathbf{\bar{x}}_k$ 가 따르는 모델을 표현하기 위해서 기존 시스템에 평균을 취하면, 아래 그림처럼 noise만 없는 동일한 시스템이 나오게 됩니다. deterministic 한 값인 $\mathbf{\bar{x}}_k$ 를 알 수 없기 때문에 이 모델은 stochastic 한 값인 $\mathbf{\hat{x}}$ 가 따른다고 가정합니다.

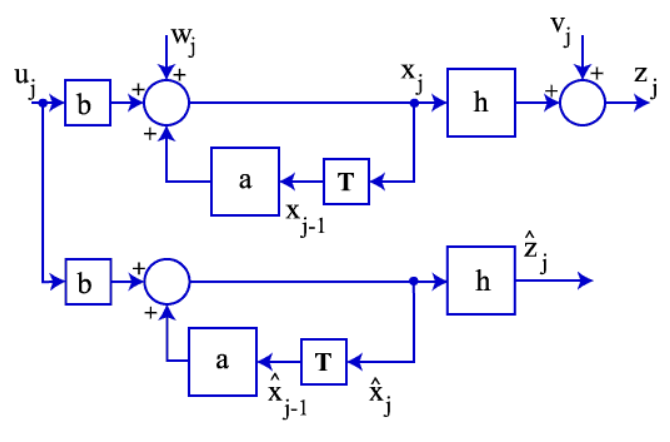출처:link

식 (8)에서 $\mathbf{\bar{x}}_k$ 대신 $\mathbf{\hat{x}^-}_k$ 을 사용하면 $\mathbf{\hat{x}}_k=\mathbf{\hat{x}}^-_k+\mathbf{C}(\mathbf{z}_k-\mathbf{H\hat{x}}^-_k)$ 이 됩니다. 이 형태를 따르도록 아래와 같이 루프를 완성시켜줍니다. 이제 추가된 모델에서 $\mathbf{C}$ 는 칼만상수 $\mathbf{K}$ 의 형태로 유도가 될 것입니다.

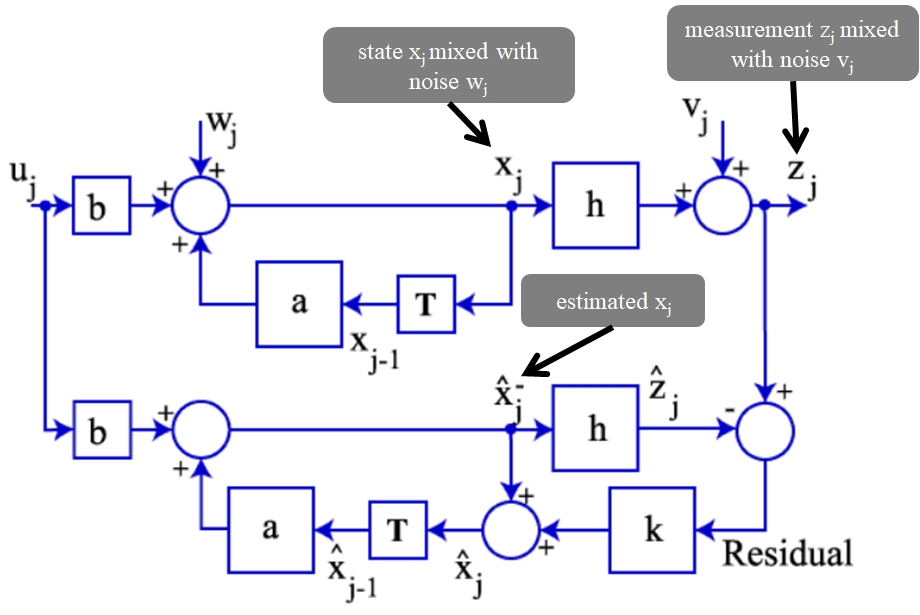출처:link

4-2. Replace $\mathbf{Q}$ with $\mathbf{P}$

위 블록 다이어 그램이 의미하는 것은, 처음에는 문제를 $\underset{\mathbf{x}}{\operatorname{argmax}}$ $p(\mathbf{x}|\mathbf{z})$ 로 풀었지만, 실제로 필터가 동작하기 위해서 아래 모델

\[\begin{aligned} \mathbf{\hat{x}}&=\mathbf{a\hat{x}+bu}\\ \mathbf{\hat{z}}&=\mathbf{H\hat{x}}\\ \end{aligned}\]

이 추가된 상황에서 $\underset{\mathbf{\hat{x}}}{\operatorname{argmax}}$ $p(\mathbf{\hat{x}}|\mathbf{z})$ 를 구한것입니다. 즉,

	$\quad$ $\quad$ $\quad$ $\quad$ Original $\quad$ $\quad$ $\quad$ $\quad$	$\quad$ $\quad$ $\quad$ $\quad$ Validated $\quad$ $\quad$ $\quad$ $\quad$
Problem statement	$\underset{\mathbf{x}}{\operatorname{argmax}}$ $p(\mathbf{x}\mid\mathbf{z})$	\(\underset{\mathbf{\hat{x}}}{\operatorname{argmax}}p(\mathbf{\hat{x}}\mid\mathbf{z})\)
Modeling	$\mathbf{x}=\mathbf{ax+bu+w}$ $\mathbf{z}=\mathbf{Hx+v}$	$\mathbf{x}=\mathbf{ax+bu+w}$ $\mathbf{z}=\mathbf{Hx+v}$ $\mathbf{\hat{x}}=\mathbf{a\hat{x}+bu}$ $\mathbf{\hat{z}}=\mathbf{H\hat{x}}$

이제 validated model에 맞게 다시 식을 수정해주면 되는데, 바뀔거는 많이 없습니다. 왜냐하면 $\underset{\mathbf{\hat{x}}}{\operatorname{argmax}}$ $p(\mathbf{\hat{x}}|\mathbf{z})$ 를 최대화 하는 추정치를 구하는 과정에서 기존과 바뀐 점은 $\mathbf{x}$ 대신 $\mathbf{\hat{x}}$ 의 확률 분포를 사용하는 것 말고 없기 때문입니다. 칼만필터는 unbiased estimator 로 $E[\mathbf{\hat{x}}_k]=\mathbf{\bar{x}}$ 가 성립함을 이미 보였고, 공분산 값만 $\mathbf{Q}$ 대신 다른 값을 써주면 됩니다. 즉, 아래 물음표에 해당하는 공분산 값을 찾으면 됩니다.

\[\begin{aligned} \mathbf{x}\sim{}N(\mathbf{\bar{x}},\mathbf{Q}) \rightarrow \mathbf{\hat{x}}\sim{}N(\mathbf{\bar{x}},\mathbf{?}) \end{aligned}\]

단순하게 생각하면 식 (8)의 결과를 이용하여 $E[(\mathbf{\hat{x}}-\mathbf{\bar{x}})(\cdots{})^T]$ 를 계산하여 나온 값을 쓰면 될 것 같습니다. ($\mathbf{C}(\mathbf{HQH}^T+\mathbf{R})\mathbf{C}^T$ 라는 값이 나옴) 하지만 의미를 알기 힘든 난해한 결과가 나오며, 보통은 추정 오차 공분산 값 $\mathbf{P}$ 를 사용합니다. 왜냐하면, 추정오차 $\mathbf{x}-\mathbf{\hat{x}}$ 에는 $\mathbf{x}$ 가 가지고 있는 process의 noise $\mathbf{w}$가 섞여 있을 텐데, 추정 오차의 크기에 대한 공분산 값을 구하는 과정에서 평균값이 0인 process noise가 미칠 영향은 미미할 것이기 때문입니다.

결론적으로 아래의 pdf를 가지는 추정치에 대해서 식을 수정하면 됩니다.

\[p(\mathbf{\hat{x}})=\frac{1}{(2\pi)^{n/2}|\mathbf{P}|^{1/2}}exp\biggl[-\frac{1}{2}(\mathbf{\hat{x}-\bar{x}})^T\mathbf{P}^{-1}(\mathbf{\hat{x}-\bar{x}})\biggr]\]

4-3. Valdation results

그럼 4-1과 4-2의 결과를 통해서 앞에서 유도된 결과에서 차례차례 바꿔보도록 하겠습니다. 또한, 같은 시점에서 update된 값을 윗첨자에 +를, update되기 전의 값엔 윗첨자 -를 사용해서 표시하겠습니다. 먼저 식 (8)은

\[\mathbf{\hat{x}}_k^+=\mathbf{\hat{x}}_k^-+(\mathbf{P}_k^-{^{-1}}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}(\mathbf{z}_k-\mathbf{H\hat{x}})\]

여기서 $(\mathbf{z}-\mathbf{H\hat{x}})$ 앞에 붙어 있는 항을 칼만상수라고 하며,

\[\mathbf{K}_k=(\mathbf{P}_k^-{^{-1}}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}\]

입니다. 이 형태는 [matrix inversion lemma]를 이용하면 다음과 같이 나타낼 수 있습니다.

\[\begin{aligned} \mathbf{K}_k&=(\mathbf{P}^{-1}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\mathbf{H}^{T}\mathbf{R}^{-1}\\ &=\{\mathbf{P}-\mathbf{PH}^T(\mathbf{R}+\mathbf{HPH}^T)^{-1}\mathbf{H}\}\mathbf{H}^T\mathbf{R}^{-1}\\ &=\mathbf{PH}^T\{\mathbf{R}^{-1}-(\mathbf{R}+\mathbf{HPH}^T)^{-1}\mathbf{HPH}^T\mathbf{R}^{-1}\}\\ &=\mathbf{P}_k^-\mathbf{H}^T(\mathbf{R}+\mathbf{H}\mathbf{P}_k^-\mathbf{H}^T)^{-1} \end{aligned}\]

식 (9)는

\[\begin{aligned} \mathbf{P}_k^+&=(\mathbf{P}_k^-{^{-1}}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\\ &=(\mathbf{I-K}_k\mathbf{H})\mathbf{P}_k^-(\mathbf{I-K}_k\mathbf{H})^T+\mathbf{K}_k\mathbf{R}\mathbf{K}_k^T \end{aligned}\]

식(5)는 애초에 $\mathbf{M}$ 을 사용하지 않은 식으로 그대로 $\mathbf{K}=\mathbf{PH}^T\mathbf{R}^{-1}$ 입니다. 하지만 주의할 점이, 그 결과가 update가 시행된 $\mathbf{P}_k^+$ 에 대해서 유도되었으므로 $\mathbf{K}_k=\mathbf{P}_k^+\mathbf{H}^T\mathbf{R}^{-1}$ 입니다.

실제로 필터를 작동시킬 때는 초기 추정치 $\mathbf{\hat{x}}_0$ 이 deterministic 한 $\mathbf{\bar{x}}_k$ 처럼 행동하진 않아 모델링 에러가 발생하겠지만, 초기 추정치 $\mathbf{\hat{x}}_0$ 과 $\mathbf{x}_0$ 의 평균의 차이가 어느정도 작고, 초기 추정 오차 공분산 값 $\mathbf{P}_0$ 를 이 오차를 커버할 수 있을 정도로 넉넉하게만 잡아준다면 오차 공분산 $\mathbf{P}$ 가 작아지면서 필터는 만족할 정도로 잘 돌아갑니다. 바꿔말하면 초기 추정치 $\mathbf{\hat{x}}_0$ 를 터무니 없이 잡거나 그에 상응하는 $\mathbf{P}_0$ 값을 설정하지 않는다면, 추정치는 이상한 값으로 발산해버립니다.

5. Conclusion

결론적으로, 유도된 결과는 다음과 같습니다. \(\begin{align} \mathbf{\hat{x}}_k^+&=\mathbf{K}_k(\mathbf{z}_k-\mathbf{H\hat{x}}_k^-)\tag{10} \end{align}\)

\[\begin{align} \mathbf{K}_k&=\mathbf{P}_k^-\mathbf{H}^T(\mathbf{R}+\mathbf{H}\mathbf{P}_k^-\mathbf{H}^T)^{-1}\\ &=\mathbf{P}_k^+\mathbf{H}^T\mathbf{R}^{-1}\tag{11} \end{align}\] \[\begin{align} \mathbf{P}_k^+&=(\mathbf{P}_k^-{^{-1}}+\mathbf{H}^T\mathbf{R}^{-1}\mathbf{H})^{-1}\\ &=(\mathbf{I-K}_k\mathbf{H})\mathbf{P}_k^-(\mathbf{I-K}_k\mathbf{H})^T+\mathbf{K}_k\mathbf{R}\mathbf{K}_k^T\tag{12} \end{align}\]

그리고, 위의 유도된 결과들은 real world에 대한 모델링에서만 유도된 게 아니라, $E[\mathbf{\hat{x}}_k]=\mathbf{\bar{x}}_k$ 라는 unbiased estimator에 대한 가정이 성립 하는 estimation 전용 모델이 추가된 상황에서 유도된 것임을 명심합시다. (아래 그림 참고)

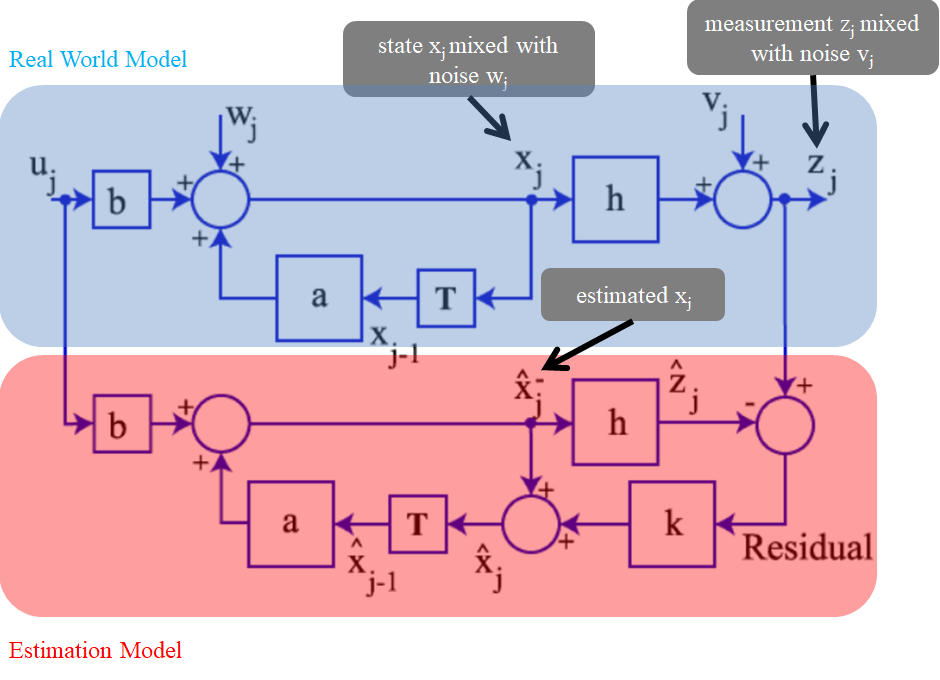
즉, 우리가 구하고 있는 추정치는 빨강색 영역의 모델을 따르고 있는 것이며, 파랑색 영역의 real world로 부터 얻은 measurement $\mathbf{z}_k$ 를 이용해서 추정치를 계속해서 구하는 것입니다.

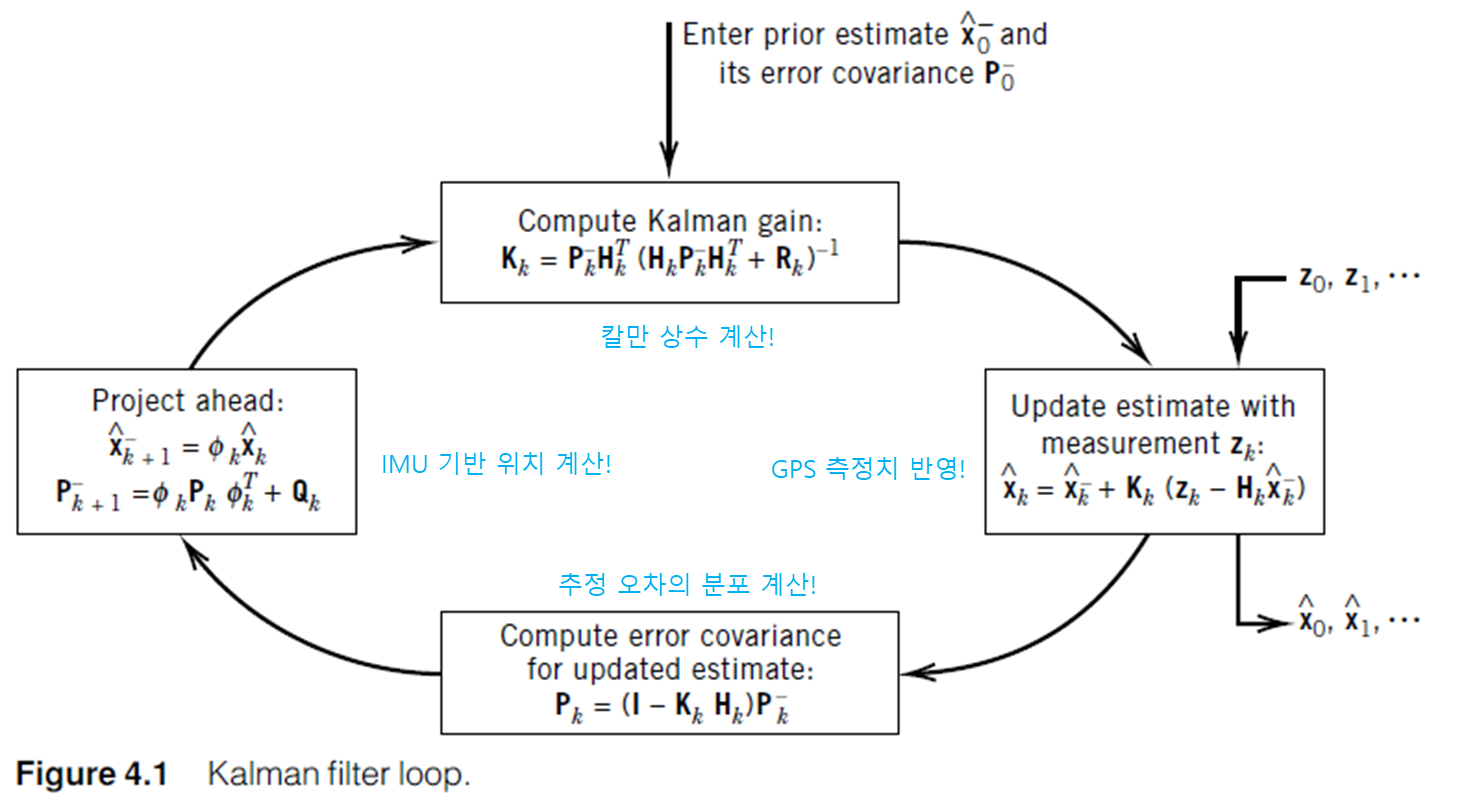
현재 유도한 과정은 칼만 필터 루프에서 measurement update가 이루어질 때의 과정을 유도한 것에 불과합니다. 시간에 대한 update는 다음 포스트 때 다루도록 하겠습니다.