말로 설명해보는 칼만필터

칼만 필터를 검색해봤다면, 아마도 전자과나 기계쪽을 전공하시는 공대생일 겁니다. 이 글에서는 칼만 필터가 왜 ‘필터’로 불리는지, 그 원리가 간단하게 어떤 건지 설명해보겠습니다.

0. 왜 이름이 필터?

필터하면 가장 먼저 생각나는게 커피 필터, 혹은 공기청정기에 들어가는 필터일 겁니다. 커피 필터는 커피콩의 찌꺼끼를 여과하고, 공기청정기 필터는 먼지를 여과합니다. 그러면 칼만 필터는 뭘 걸러낼까요? 아래 칼만 필터에 대한 비유를 기가 막히게 해준 그림이 있습니다.

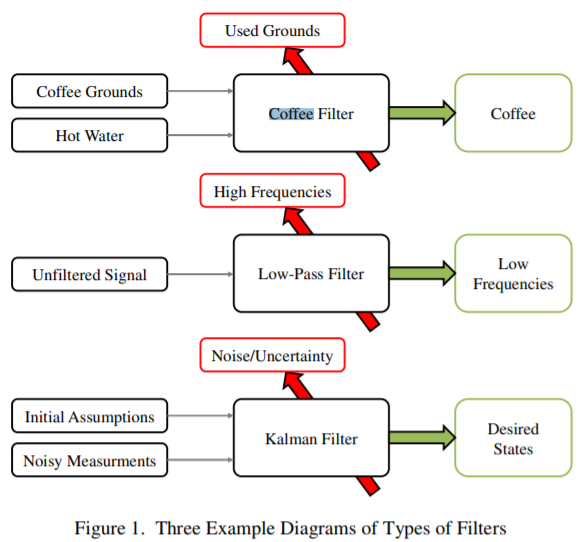
그림에서 보다시피, 초기 추정치 (Initial Assumption)와 잡음이 섞인 측정치 (Noisy Measurements)가 칼만필터를 통과하면, noise와 불확실성이 걸러진, 조금 더 깔끔해진 추정치를 얻을 수 있게 됩니다. 이게 뭔 소리냐고요?

우린 현실세계에서 어떤 값을 추정할 뿐이지, 절대로 참값을 알 수 없습니다. 예를 들어 신발 사이즈를 정하기 위해, 가지고 있는 1mm 눈금자로 발바닥 길이를 잰다고 해보죠. 여러분은 눈금자로 ‘대강’의 치수를 측정할 뿐이지 ‘참값’을 알아내는게 아닙니다. 그렇기 때문에 모든 측정치에는 일정 수준의 잡음이 섞이게 됩니다. 신발 사이즈를 잴 때 잡음의 크기는 커봤자 1mm 정도겠네요.

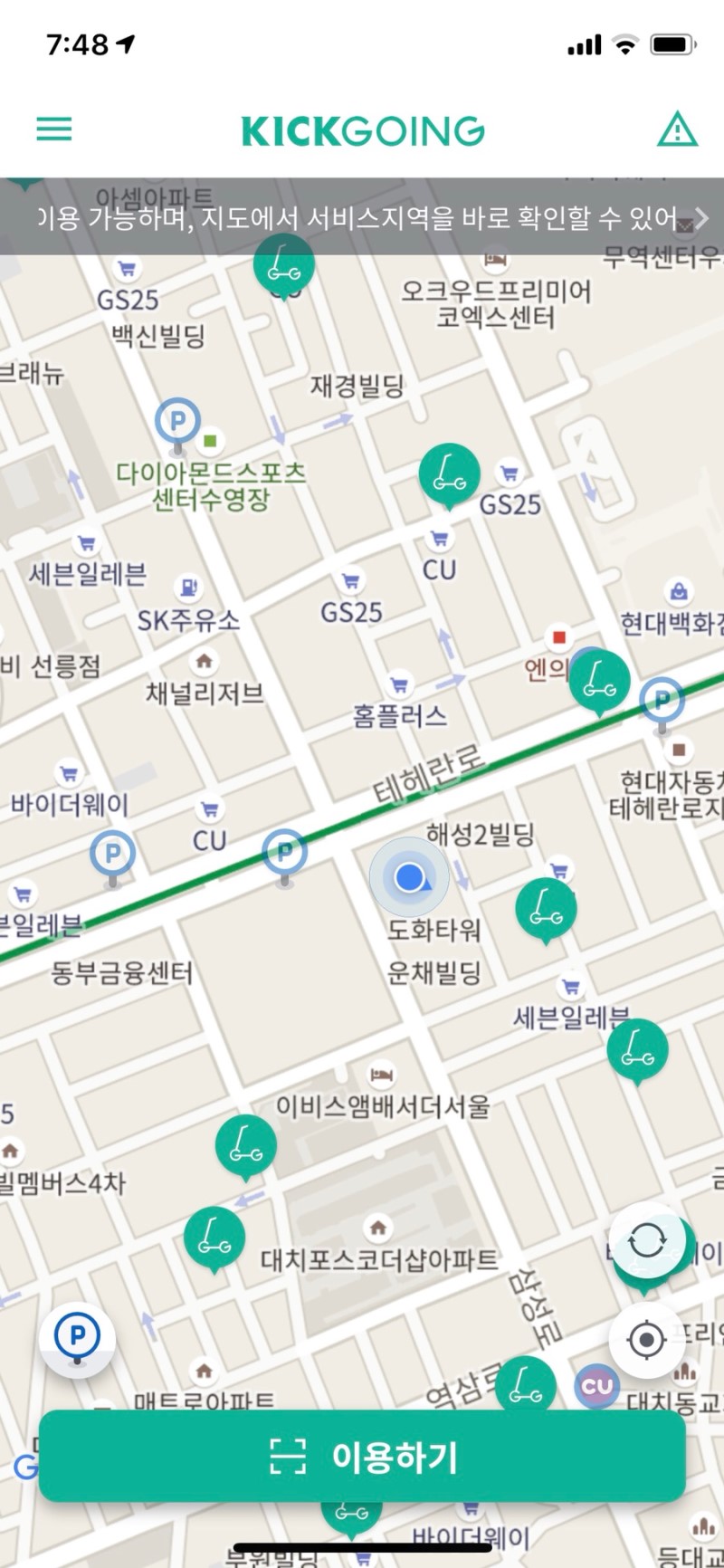
이번엔 요새 흔히 보이는 전동 킥보드를 생각해봅시다. 여러분은 전동 킥보드를 찾기 위해 여러분의 위치와 킥보드의 위치를 함께 보여주는 어플을 켰습니다. 어플은 핸드폰 내에 장착된 움직임 감지 센서 (IMU, Inertial Measurement Unit)와 GPS 수신기로부터 여러분의 위치를 계산하기 시작합니다. 하지만 앞서 말했듯이 센서를 비롯한 측정 기구들은 반드시 측정 오차에 의한 잡음을 포함하고 있습니다. 하지만 이 정보들을 칼만필터에 통과시키면? 추정에 사용되는 정보들의 잡음이 어느정도 걸러지면서 최종적으로 위치값을 더 정밀하게 추정할 수 있게 됩니다.

앞에서 예시를 든 전동 킥보드 어플 말고도, 칼만 필터가 사용되는 분야는 매우 많습니다. 센서를 활용하는 모든 분야가 되겠네요. 결국 칼만필터는 시스템에 사용되는 센서의 정보를 깔끔하게 정제하기 위해 필요한 기법이라고 할 수 있습니다.

1. 칼만필터는 어떻게 만드나요?

결론 부터 얘기하자면, 복잡한 수식에 의해 구성됩니다. 하지만 수식을 설명하기 보다는, 수식이 말하고자 하는 것을 설명드리고자 합니다.

먼저 원리를 이해하기 전에 평균과 표준편차의 개념을 아셔야 합니다. 평균은 여러분이 학창 시절 평균 점수를 내기 위해서도 많이 구해보셨을 텐데요, 데이터들의 대표값이라고 생각하시면 편할 것 같습니다. (물론, 평균이 데이터들을 가장 잘 나타내는 값은 아니지만) 표준 편차는 평균값을 중심으로, 데이터들이 어떻게 분포 되어 있는지를 말해주는 지표입니다. 예를 들어 어느 고등학교 1학년 전교생의 국어성적이 있을 때, 전교생이 다 컨닝을 해서 모두 점수가 50점이라면, 평균은 50점이고 표준 편차는 0입니다. 하지만 정상적으로 시험을 쳐서 평균은 똑같이 50점인데 0점부터 100점까지 고루고루 분포가 되어있다면, 표준 편차는 0보다 큰 값을 가지게 될 것입니다. 보통 표준 편차 값의 3배 정도에 거의 모든 데이터가 분포하기 때문에, 대충 계산해보자면 50/3 = 17 정도가 표준편차가 될 것입니다.

자, 그럼 다시 전동 킥보드 문제로 돌아가봅시다. 앞에서 사용자의 움직임을 측정하는 센서인 IMU와 GPS 센서의 측정치를 사용해서 위치를 추정한다고 했는데, 각각의 측정치는 잡음에 의한 표준편차를 가지게 됩니다. 여러분이 제자리에 가만히 서있다고 하더라도, GPS의 경우 그 위치를 중심으로 오차를 가지는 측정치가 찍힐테고, IMU의 경우 가속도 값이 0을 중심으로 분포하겠네요. 대충 수식으로 나타내면 아래와 같습니다.

    다음위치 = 지금위치 + 잡음이 섞인 IMU로부터 적분한 값
    GPS 측정치 = 지금위치 + GPS 잡음

그럼 이 두 정보를 어떻게 합쳐야 할까요? 한 번은 IMU 정보를 기반으로 위치를 계산하고 (가속도 값을 두 번 적분!) 다른 한 번은 GPS 정보만 믿어야 할까요? 아니면 두 정보를 단순하게 평균낼까요? 칼만 상수에 의한 정보량의 혼합은 아래와 같은 형태로 이루어집니다.

    보정된 위치 = IMU로만 계산한 보정 전 위치 + 칼만 상수(GPS측정치 - IMU로만 계산한 보정 전 위치)

위 식이 합리적인 것 같나요? IMU와 GPS 정보가 둘 다 들어간 것 같긴 한데 왜 저런 형태로 보정을 할까요? 사실, 위 식은 결과적인 형태이고 실제로는 확률 분포의 likelihood(우도)값을 최대화 하는 과정에서 위와 같은 형태의 식이 나오게 됩니다. 그 과정을 다 설명하긴 너무 복잡하니, ‘위와 같은 형태로 보정되는구나’ 하고 넘어가시면 될 것 같습니다. 다만, 위 식과 같이 보정을 할 때 문제는 칼만 상수를 어떻게 설정하면 될까라는 것이죠

답을 해드리자면 칼만 필터는, 정보를 합했을 때 얻어지는 추정 오차를 최소화 하도록 구성됩니다. 추정 오차를 최소화 하도록 하는 칼만 상수를 구하면, 결론적으로 추정 오차의 표준 편차가 점점 줄어들게되어, 원하는 참값에 근접한 추정치를 구할 수 있게 됩니다. 여태까지 말로만 줄줄 적어 내려갔는데, 이제 식으로 표현을 해보면 아래 그림과 같습니다.

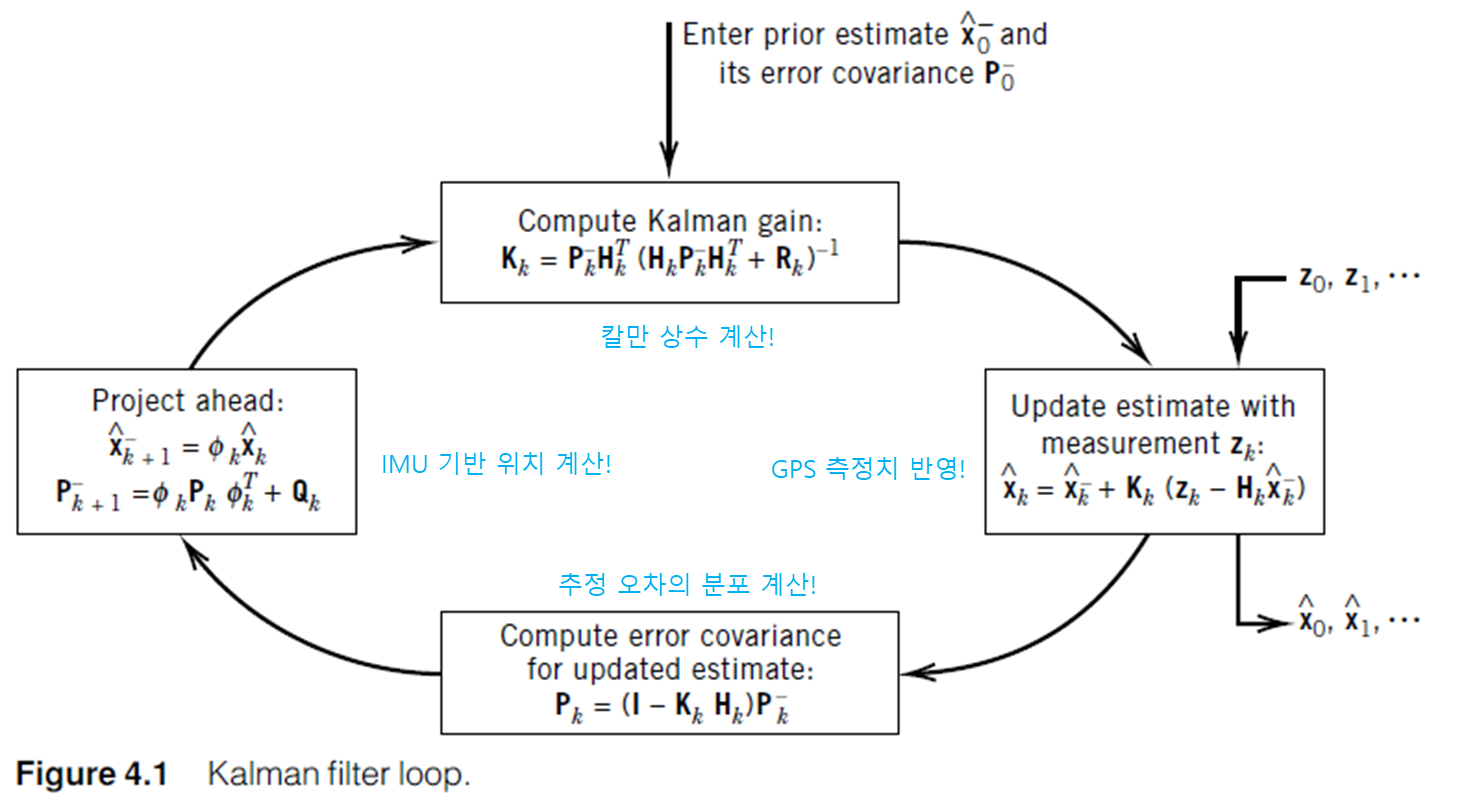
네… 수식으로 보면 어려워 보이지만, 결국 수식으로도 말하고자 하는 것은 내가 센서 A와 B로 어떤 값을 추정하고자 한다면, 다음의 절차를 따른다는 것입니다.

    1. 한 센서로 러프하게 추정값 계산
    2. 추정 오차를 최소화 하는 칼만 상수 계산
    3. 다른 센서의 값을 칼만 상수를 통해 반영하여 보정
    4. 보정하고 나서 (줄어든) 추정 오차의 분포 계산

결국 1 ~ 4를 계속 반복하는 것에 불과하고, 위 루프가 결국 센서의 잡음에 의한 불확실성을 줄여주는 필터의 구조라고 보시면 됩니다. 결국에는 추정 오차값이 줄어들게 되니까요. 센서의 갯수가 늘어나거나 추정하는 값이 내 위치 뿐만 아니라 속도, 방향각, 센서의 바이어스와 같이 늘어나면 그에 맞게 식을 재구성해주면 되는 것입니다.

2. 칼만 필터에도 종류가 있나요?

네, 칼만 필터의 종류에도 여러 가지가 있습니다. 생각해보니 지금 코로나 때문에 쓰는 마스크도 필터인데, 마스크에도 KF94, KF80, 덴탈 마스크 등 여러가지가 있네요. 칼만 필터도 다른 여러 가지 종류가 있으며, 우리가 쓰는 마스크처럼 각각의 성능이 다릅니다. 칼만 필터의 입장에서는, 추정 오차를 줄여 주는게 성능이니까 다른 종류의 필터 마다 추정 오차가 줄어드는 양상이 달라지겠군요.

먼저 칼만 필터의 종류들을 나열하자면, 확장형 칼만 필터 (EKF, Extended Kalman Filter), 무향 칼만 필터 (UKF, Unscented Kalman Filter), 파티클 필터 (PF, Particle Filter), 입체구적 칼만 필터 (CKF, Cubature Kalman Filter)가 있습니다. 이 필터들은 시스템의 비선형성에 의해 성능이 갈리게 됩니다. 비선형성이란 뭘까요? 선형적이지 않은것? 그럼 선형적인 건 뭘까요? 선…? 막대기? 일자..?

선형 시스템은 수학적 정의로 ‘입력과 출력이 선형성을 만족하는 시스템’으로 (뭐야…), 여기서 선형성이란 상수곱과 합의 연산에 관한 성질을 말합니다. 중요한 건 이게 아니고, 쉽게 표현하면 선형 시스템은 ‘내가 생각한 대로 예측이 가능한’ 쉬운 시스템이란 것입니다. 예를 들어, 자동차와 드론을 예를 들어 볼까요. 자동차의 경우 도로를 따라 보통 직선으로 움직이기 때문에 위치를 예측하기 쉽습니다. 만약 속도 제한이 100인 고속도로를 차선 변경 없이 달린다고 생각하면, 자동차의 위치는 그 차선을 벗어나지 않는 선에서 적당하게 예측을 할 수 있죠. 하지만 드론의 경우 얘기가 많이 다릅니다. 우선 드론은 중량이 훨씬 작기 때문에 바람과 같은 외부 요인에 의한 영향도 받고, 드론 택배와 같이 짐을 나르게 될 때 무게 중심도 변합니다. 만약에 나르는 물체가 액체라면요? 그럼 더 예측하기 힘든 방향으로 움직일 가능성이 높습니다. 또한 이동 시 항상 자세를 바꾸는 식으로 (앞으로 기울기, 옆으로 기울기) 움직이기 때문에 자동차보다 비선형성이 높은 시스템이라고 말할 수 있습니다.

이렇게 시스템의 특성에 따라 비선형성이 달라지기 때문에 비선형성을 고려한 필터의 설계가 필요합니다. 쉽게 말하자면, 위에서 나열한 필터에서 EKF와 UKF를 사용할 때, UKF가 비선형성을 더 잘 고려하기 때문에 EKF를 사용할 때 보다 추정 오차가 빠르게 줄어들고, 더 많이 줄어들 여지가 있습니다. 그럼 무조건 성능 좋은 필터를 구현하는게 능사일까요? 우리가 비말 마스크보다 KF94마스크를 끼고 운동할 때 더 힘든 것처럼, 비선형성을 더 잘 고려한 필터를 사용할 수록 연산량이 증가한다는 단점이 존재합니다. 만약 1초에 100번의 데이터를 주는 IMU를 사용하는 경우, 그 속도에 맞춘 연산을 수행해야 하는데 UKF는 연산속도가 정보의 입력 속도를 따라가지 못하는 문제가 발생할 수 도 있는 것이죠!

3. 맺음말

대학원에서 전공한 내용을 최대한 알기 쉽게 정리해 보았는데요, 수식 사용을 자제한 상태로 칼만 필터에 대한 설명을 해보았는데, 내용이 잘 전달되었나 모르겠습니다. 부족하거나 이상한 부분이 있다면 피드백 부탁드립니다!

참고문헌

1. M. B. Rhudy, R. A. Salguero, K. Holappa, “A Kalman filtering tutorial for undergraduate students,” International Journal of Computer Science & Engineering Survey, vol. 8, no. 1, pp 1-18, 2017

2. R. G. Brown, P. Y. C. Hwang, “Introduction to random signals and applied Kalman filtering: with MATLAB exercises 2nd ed.,” New York, NY: Wiley, 1992