Bayes Filter - 모든 필터의 근본

Overview

Bayes filter, 또는 recursive Bayesian estimation은 측정치와 process model을 사용하여 원하는 state의 probability density(continuous), 혹은 distribution(discrete)을 추정할 수 있는 가장 일반적인 관측기로, 유명한 Kalman Filter를 비롯한 모든 확률 기반 추정 알고리즘은 여기서 파생되었다. Kalman Filter는 선형 시스템의 Bayes filter에다 Gaussian 형태의 잡음 분포를 사용한 최적 형태의 관측기일 뿐이다.

Why Bayes Rule ‘rules?’

Bayes filter의 근간에는 Thomas Bayes 가 제안한 Bayes rule이 기본이 되며, 식의 형태는 단순해 보이지만 그 의미는 통계적으로 매우 의미가 있다. 아래 식을 보자. (continous 한 시스템으로 가정하고 설명)

\[\begin{align} p(x\vert y) &= \frac{p(y\vert x)p(x)}{p(y)}\tag{1} \end{align}\]

여기서 x는 우리가 추정하고 싶은 state이고, y는 경험에 의해서 (전자시스템이면 센서, 여론 조사와 관련된 거면 전화 응답 결과, 등) 관측된 측정치이다. 식만 보면 형태는 단순한 것 같다. 조건부 확률의 정의만 알고 있다면, 등호가 성립하는 것은 간단하게 이해할 수 있다.

이제 통계적인(또는 공학적인) 마인드로 식 (1)의 좌변을 살펴보자. 경험적으로 얻은 값 y가 주어질 때 x의 probability density 값을 뜻한다. 경험적으로 얻은 값을 통해 어떤 것을 알고자 하는 행위는 귀납적인 방식으로, 이는 최대한 표본이 많을 수록 그 정확도가 올라간다. 하지만 보통 현실적인 한계 (대통령의 긍정 평가율을 알기 위해 전국민에게 전화를 돌리지는 않는 것 처럼)에 부딪히게 되기 때문에, 원하는 state의 probability density를 구할 때는 일부의 데이터만 취득하게 된다.

이제 (1)의 우변에 있는 $p(y\vert x)$를 유심히 들여다 보자. 추정하고 싶은 state가 주어질 때 경험적으로 얻게 되는 값의 확률 분포이다. 아직 state를 추정하기도 전인데 얘는 도대체가 어떻게 구할 수 있다는 걸까? 라고 생각할 수 있지만 이 값이야 말로 우리가 합리적으로 구할 수 있는 값이다. state를 추정하지는 않았지만, state가 어떤 값이라고 가정했을 때 경험적으로 얻을 수 있는 y는 실생활에서 찾아볼 수 있다.

앞에서 예를 든 것처럼 대통령의 긍정평가율을 조사한다고 하자. 여기서 state는 positive, 혹은 negative로 우리는 전화를 돌려서 사람들에게 아마 다음과 같이 물어볼 것이다. ‘대통령이 잘하고 있다고 생각하십니까?’ 이는 곧 $y\vert x=positive$ 에 대한 샘플을 얻은 것이다. 우리는 동전을 던지는 횟수가 많아지면, 앞/뒤가 나올 확률이 0.5에 가까워진다는 큰 수의 법칙을 알고 있기 때문에, 전화를 10000통 정도 돌리면 $p(y\vert x=positive)$ 혹은 $p(y\vert x=negative)$ 에 대한 적당한 값이 나올 것이라고 예상할 수 있다.

센서로 예를 들어보자. 가속도와 각속도(state)를 측정하는 IMU의 경우, 센서를 장치에 고정시켜서 가속도 및 각속도를 0의 상태로 만들 수 있다($\mathbf{x = 0}$). 실제로 만들어진 센서는 아무리 잘 만들어져도 고정된 상태에서 각속도 및 가속도가 0이 나오지 않기 때문에, 오랜 시간동안 놔두면 측정된 가속도 및 각속도에 의해 센서가 움직인 것 처럼 측정되게 된다. IMU의 잡음(noise)는 이런식으로 측정하여 $p(y\vert x)$는 gaussian 형태로 가정하여 product sheet에 기록되게 된다. 비단 IMU 뿐만 아니라 만들어지는 모든 센서들은 제작 후 위와 비슷한 과정으로 noise의 분포를 측정하도록 되어있다.

참고로 이렇게 경험에 의해서 측정할 수 있는 $p(y\vert x)$는 x가 주어질 때 측정치 y의 조건부 확률, 또는 x의 measurement likelihood(우도) 라고 한다. 조건부 확률은 우도의 표현식으로, 둘의 미묘한 차이에 대해서 알고 싶다면 여기를 참고하도록 한다.

한편 식 (1)의 우변에서 분모를 Total Probability Theorem에 의해서 아래와 같이 나타낼 수 있다.

\[\begin{align} p(x\vert y) &= \frac{p(y\vert x)p(x)}{p(y)}\\ &=\frac{p(y\vert x)p(x)}{\int{p(y\vert x')p(x')dx'}}\tag{2} \end{align}\]

적분기호가 있어서 어려워 보이지만 아래 그림처럼 discrete system에서 total probability theorem을 본다면 쉽게 이해할 수 있다.

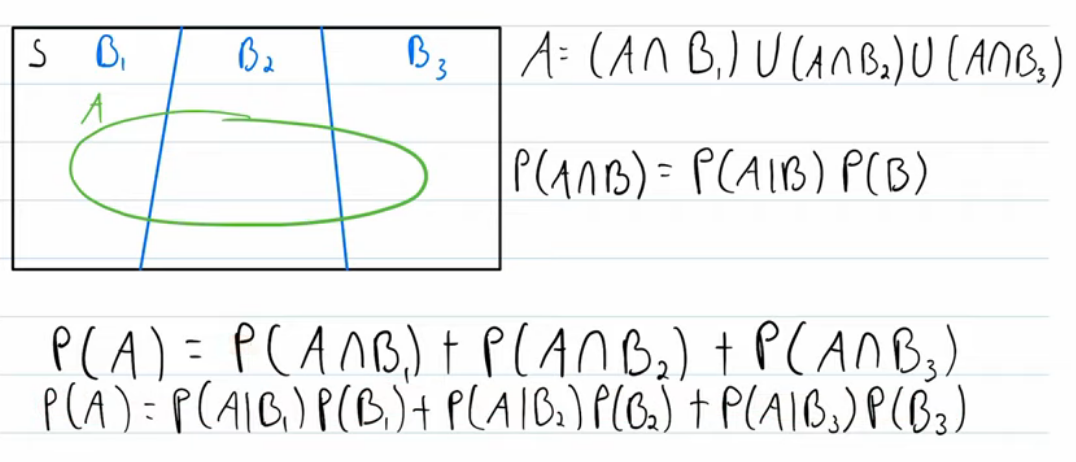reference:Youtube:Wrath of Math

Bayes Filter

Bayes Filter는 위에서 설명한 Bayes rule을 기반으로 측정치 및 시간의 흐름에 따라 recursive하게 state를 추정하도록 짜여진 알고리즘이다.

Modelling

추정하고자 하는 state x의 시간의 흐름에 따른 변화와 한 시점에서 측정된 측정치 z에 대해서 아래와 같이 process equation(식(3))과 measurement equation(식(4))를 구성할 수 있다. 여기서 w 및 v는 입력 및 측정치에 섞인 noise를 뜻한다.(Kalman Filter를 유도하는 과정이라면 noise인 $\mathbf{w}$ 와 $\mathbf{v}$ 의 분포를 Gaussian으로 가정하는 등의 절차가 있겠지만, 여기서는 확률 분포를 따로 특정하지 않고 general한 경우에 대해서 문제를 풀도록 해본다.)

\[\begin{align} \mathbf{x_{t}}&=\mathbf{Ax}_{t-1}+\mathbf{Bu}_{t}+\mathbf{w}_{t}\tag{3}\\ \mathbf{z}_{t}&=\mathbf{Hx}_{t}+\mathbf{v}_{t}\tag{4} \end{align}\]

우리가 구하는 것은 어느 시점 t에서 state x의 정확한 값이 아니라 확률 밀도값 $p(\mathbf{x_t})$ 이다. 또한, 어떤 시점 t에서 state x는 이전 시점의 값들이 존재하고 나서의 값이다. 따라서 우리가 최종적으로 구해야 하는 값은 $p(\mathbf{x_t} \mid \mathbf{u_1},\mathbf{z_1},\ldots,\mathbf{u_t},\mathbf{z_t})$ 인 것이다. 이 값은 보통 깔끔하게 $p(\mathbf{x_t} \mid \mathbf{z_{1:t}},\mathbf{u_{1:t}})$ 로 나타낸다.

Update

$p(x_t\mid\mathbf{z_{1:t}},\mathbf{u_{1:t}})$ 는 Bayes rule에 의해 다음과 같이 전개 된다.

\[\begin{align} p(\mathbf{x_t}\mid\mathbf{z_{1:t}},\mathbf{u_{1:t}}) &= \frac{p(\mathbf{z}_t\mid\mathbf{x_t},\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}{p(\mathbf{z}_t\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\tag{5} \end{align}\]

여기서 시스템이 Markov property 를 따른다고 가정하면 식 (5)를 좀 더 간단하게 나타낼 수 있다. Markov property는 한 시점 t+1에서 state x는 이전 시점($1\ldots t$)을 모두 포함한 정보를 가지고 있다는 특성으로, 그렇게 되는 경우 시점 t+1에서 state x는 $\mathbf{x_{t}}$ 와 $\mathbf{u_{t+1}}$ 만으로도 결정지을 수 있게 된다. 이해를 돕기 위해 아래 그림을 보자.

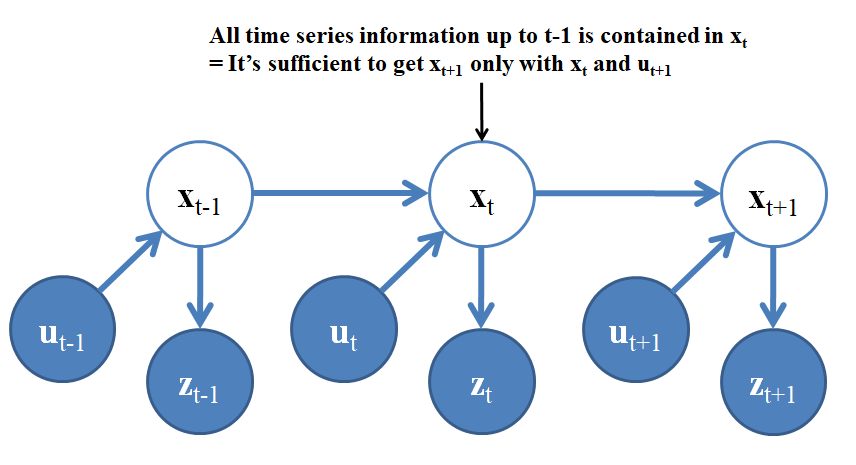
즉, $\mathbf{x_{t+1}}$ 를 결정하는데 있어서 위 그림에서 $\mathbf{x_{t}}$ 와 $\mathbf{u_{t+1}}$ 만 고려하면 이전 시점의 측정치와 input을 모두 고려한 셈이 된다는 뜻이다. 따라서 구해야 할 식 (5)는 아래와 같이 간소화 할 수 있다.

\[\begin{align} p(\mathbf{x_t}\mid\mathbf{z_{1:t}},\mathbf{u_{1:t}}) &= \frac{p(\mathbf{z}_t\mid\mathbf{x_t},\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}{p(\mathbf{z}_t\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\\ &=\frac{p(\mathbf{z}_t\mid\mathbf{x_t})p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}{p(\mathbf{z}_t\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\tag{6} \end{align}\]

또한, 확률 분포 값은 항상 적분 시 1이 되도록 설정될 것이므로 분모의 값은 간단하게 normalizing factor $\eta$ 를 사용해서 다음과 같이 더 간단하게 나타낼 수 있다.

\[\begin{align} p(\mathbf{x_t}\mid\mathbf{z_{1:t}},\mathbf{u_{1:t}}) \propto \eta\:p(\mathbf{z}_t\mid\mathbf{x_t})p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})\tag{7} \end{align}\]

식 (7)의 좌변과 우변에 있는 $p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})$ 은 $\mathbf{z}_t$ 가 반영되었는지 아닌지의 차이 밖에 없다. 따라서 위 식을 measurement 에 의한 update 라고 한다.

Prediction

식 (7)의 우변에 있는 $p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})$ 에서 $\mathbf{x_{t-1}}$ 에 대하여 total probability theorem, bayes rule, 그리고 markov property를 적용하면 아래와 같이 변형할 수 있다.

\[\begin{align} p(\mathbf{x_t}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})&=\frac{p(\mathbf{x_t},\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}{p(\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\\ &=\frac{\int{p(\mathbf{x_t},\mathbf{z_{1:t-1}},\mathbf{u_{1:t}}\mid\mathbf{x_{t-1}})p(\mathbf{x_{t-1}})}\mathbf{dx_{t-1}}}{p(\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\\ &=\frac{\int{p(\mathbf{x_t}\mid\mathbf{x_{t-1}},\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})p(\mathbf{x_{t-1}},\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\mathbf{dx_{t-1}}}{p(\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\\ &= \int{p(\mathbf{x_t}\mid\mathbf{x_{t-1}},\mathbf{u_{t}})p(\mathbf{x_{t-1}}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t}})}\mathbf{dx_{t-1}}\tag{8} \end{align}\]

식 (8)의 맨 마지막 줄에서 입력 $\mathbf{u_t}$ 은 $\mathbf{x_{t-1}}$ 과 independent 하므로 결국 아래의 식과 같게 된다.

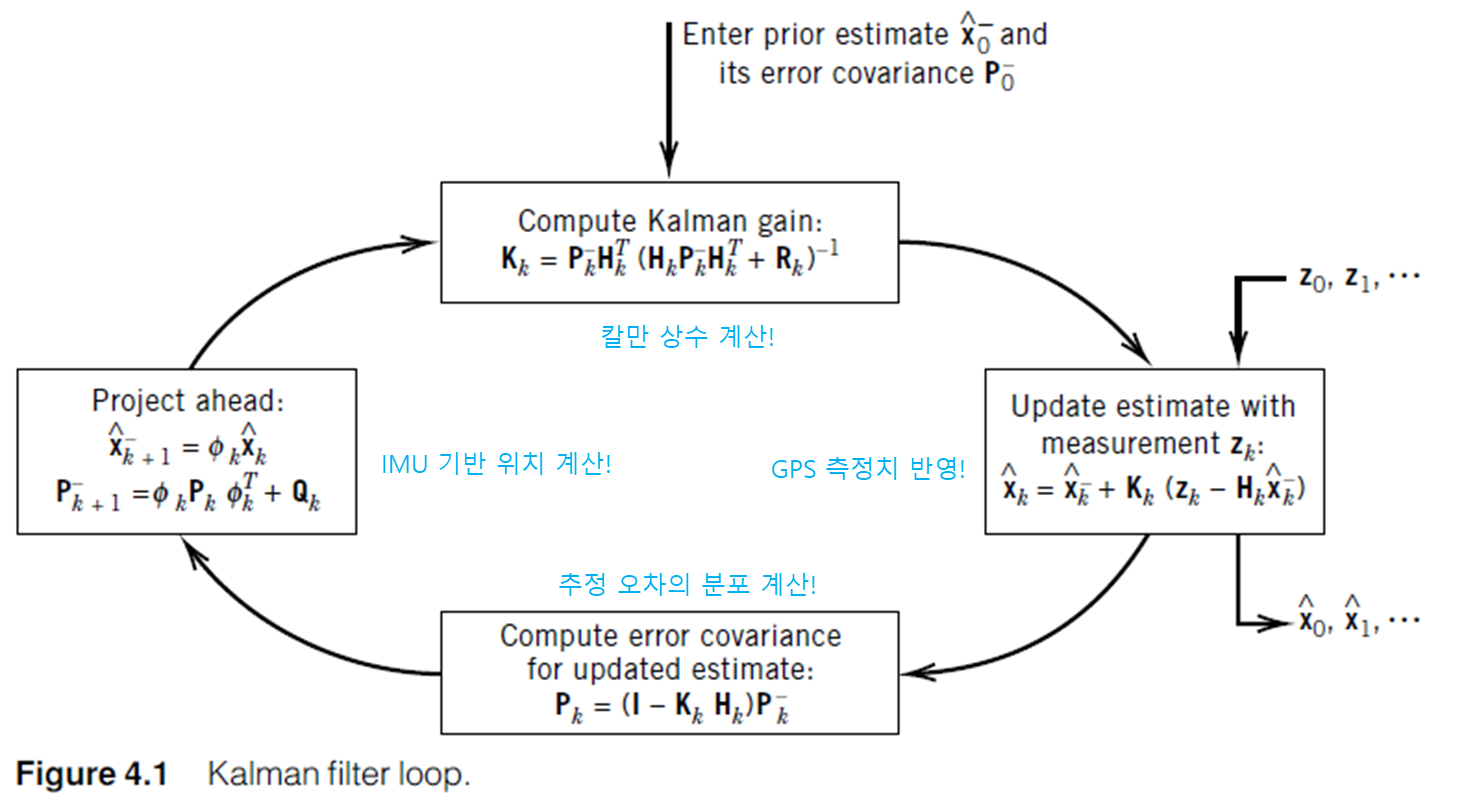
\[\begin{align} p(\mathbf{x_t}\vert\mathbf{z_{1:t-1}},\mathbf{u_{1:t}}) = \int{p(\mathbf{x_t}\vert\mathbf{x_{t-1}},\mathbf{u_{t}})p(\mathbf{x_{t-1}}\vert\mathbf{z_{1:t-1}},\mathbf{u_{1:t-1}})}\mathbf{dx_{t-1}}\tag{9} \end{align}\]

식 (9)에서 좌변과 우변의 $p(\mathbf{x_{t-1}}\mid\mathbf{z_{1:t-1}},\mathbf{u_{1:t-1}})$ 의 차이는 시점 t로 넘어가면서 control input $\mathbf{u_t}$ 가 추가되는 것 말고 없다. 따라서 위 식을 prediction 이라고 부른다.