Inertial Navigation System

1. Frame 간 벡터 표현

벡터 $\alpha$를 한 좌표계 $\beta$에서 $\psi{}$만큼 회전시킬 때 식은 아래와 같다.

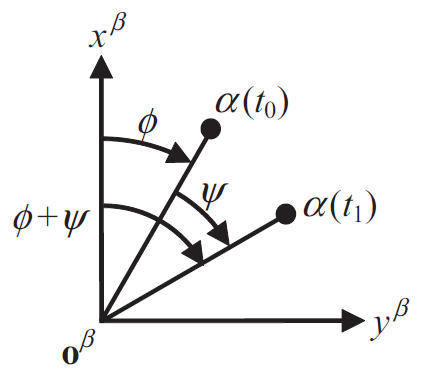
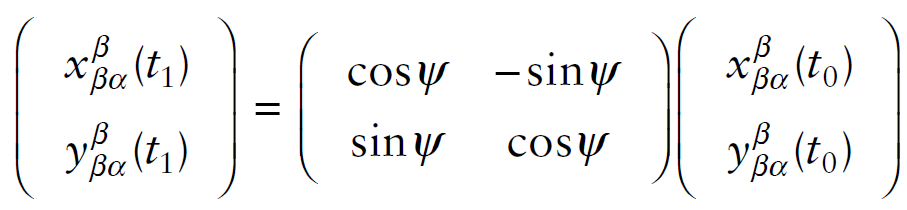
좌표계 $\beta$에 대해서 자세가 $\psi$만큼 삐딱하게 틀어진 좌표계$\gamma$로 $\alpha$를 나타내면 아래와 같다.

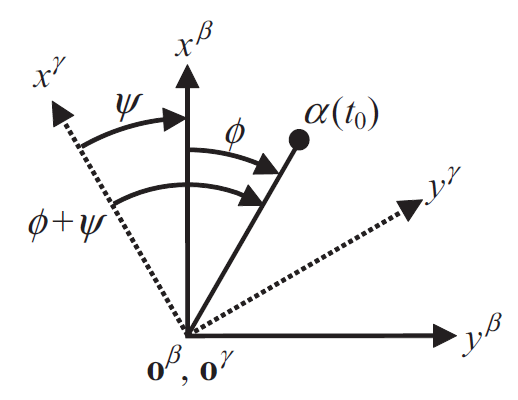
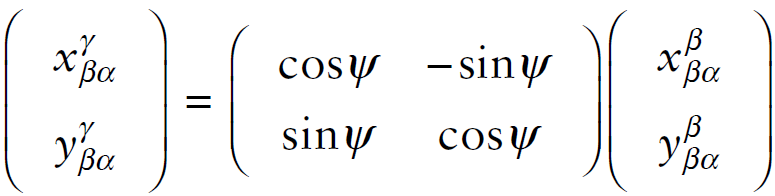
두 식 모두 동일한 변환 행렬인

\[\begin{pmatrix} cos\psi&-sin\psi\\ sin\psi&cos\psi \end{pmatrix}\]

를 볼 수 있다. 즉, 원래 좌표계(reference frame, $\beta$)에서 자세가 다른 좌표계(object frame, $\gamma$)로 벡터를 변환하려면 회전 행렬을 사용하면 된다.

object frame → reference frame에 필요한 회전량을 자세(attitude)라고 한다. 따라서 위의 그림에 따라 object frame $\gamma$의 refernce frame $\beta$에 대한 자세는 $\psi$이다.

회전을 표현하는 방식에는 아래와 같이 크게 4가지가 있다.

1.1. Euler angle

어떤 벡터를 좌표계 $\beta$에서 좌표계 $\alpha$로 표현해보자. 3차원에서 회전은 x, y, z축에 대해서 수행할 수 있으며 순서는 z축에 대한 회전($\psi_{\beta\alpha}$), y축에 대한 회전($\theta_{\beta\alpha}$), 그리고 x축에 대한 회전($\phi_{\beta\alpha}$)이 마지막으로 오도록 약속한다. 이는 아래와 같은 오일러각으로 표현된다.

\[\mathbb{\Psi}_{\beta \alpha}=\begin{pmatrix} \phi_{\beta \alpha} \\ \theta_{\beta \alpha} \\ \psi_{\beta \alpha} \end{pmatrix}\]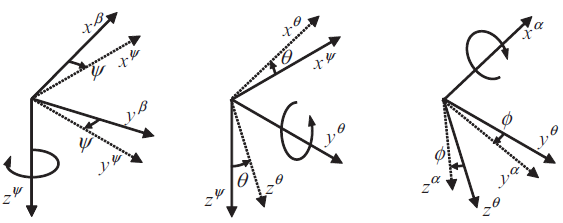

1. 좌표계 $\beta$의 z축에 대해서 좌표계를 $\psi_{\beta \alpha}$만큼 돌린다. 벡터 입장에서는 $-\psi_{\beta \alpha}$ 회전이다.

   

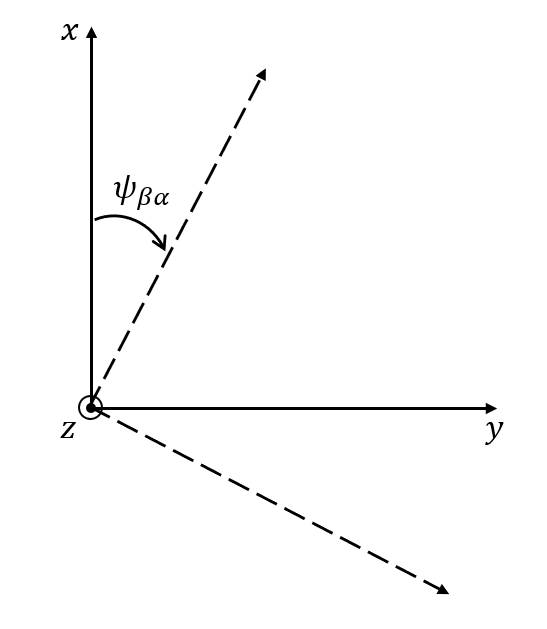
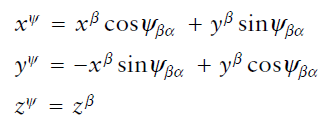
1. 돌려진 좌표계의 y축에 대해서 좌표계를 $\theta_{\beta \alpha}$만큼 돌린다.

   

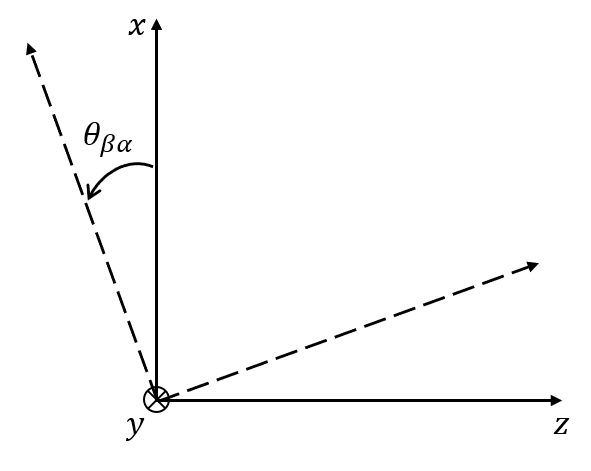
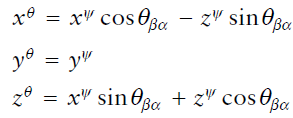
1. 돌려진 좌표계의 x축에 대해서 $\phi_{\beta \alpha}$만큼 돌린다.

   

   

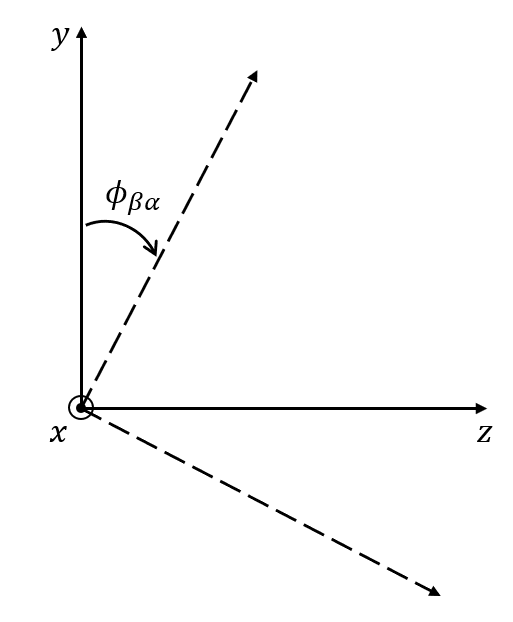
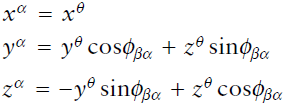
오일러각은 직관적이지만, 자세 변환에 pitch각 $\pm90\deg$ 인 변환이 포함되는 경우 무수히 많은 roll/yaw 해가 존재한다는 단점이 있다. (gymbal lock) 그래서 오일러각은 자세 계산에는 잘 사용되지 않는 표기법이다.

1.2. Coordinate transformation matrix (Direct cosine matrix)

1.1에 있는 식을 행렬로 표현하면 다음과 같다.

\[\begin{pmatrix} x^{\alpha}\\y^{\alpha}\\z^{\alpha} \end{pmatrix}= \begin{pmatrix} 1&0&0\\0&\cos{\phi_{\beta\alpha}}&\sin{\phi_{\beta\alpha}}\\0&-\sin{\phi_{\beta\alpha}}&\cos{\phi_{\beta\alpha}} \end{pmatrix} \begin{pmatrix} \cos{\theta_{\beta\alpha}}&0&-\sin{\theta_{\beta\alpha}}\\0&1&0\\\sin{\theta_{\beta\alpha}}&0&\cos{\theta_{\beta\alpha}} \end{pmatrix} \begin{pmatrix} \cos{\psi_{\beta\alpha}}&-\sin{\psi_{\beta\alpha}}&0\\\sin{\psi_{\beta\alpha}}&\cos{\psi_{\beta\alpha}}&0\\0&0&1 \end{pmatrix} \begin{pmatrix} x^{\beta}\\y^{\beta}\\z^{\beta} \end{pmatrix}\]

곱할 행렬들을 하나로 미리 계산하면

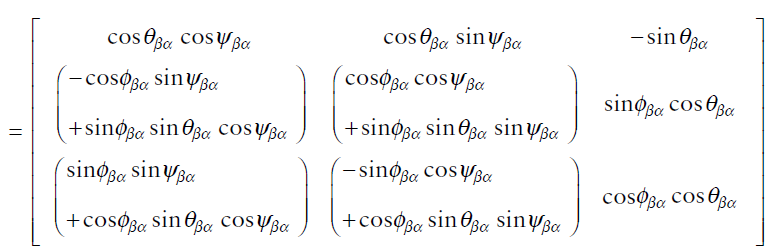
이를 Coordinate transformation matrix (DCM이라고도 함) 라고 하며, 아래 처럼 표현한다.

\[x^{\alpha}=\text{C}_{\beta}^{\alpha}x^{\beta}\]

$\text{C}_{\beta}^{\alpha}$ 가 의미하는 바는 오일러각에 의해 수행되는 세 번의 회전에 대응되는 한 번의 회전이다. DCM 1.3에서 설명하는 quaternion과 함께 회전 연산에 많이 쓰이는 표현 방식이다.

1.3. Quaternion

그렇다면 저 회전의 중심이 되는 벡터가 있을 것이다. 이는 다음의 연립방정식을 풀면 된다.

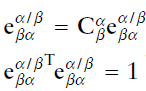
여기서 $\text{e}_{\beta\alpha}^{\alpha/\beta}$는 $\beta$에서 $\alpha$로 회전시킬 때 중심이 되는 단위 벡터로, 회전 결과 자기 자신이 되기 때문에 위와 같은 식이 성립한다.

이를 풀면 아래와 같은 결과가 얻어진다.

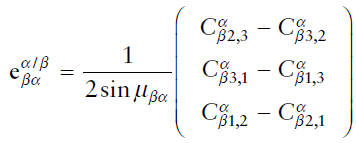
여기서 $\mu$는 회전량으로, 그 값은 아래와 같다.

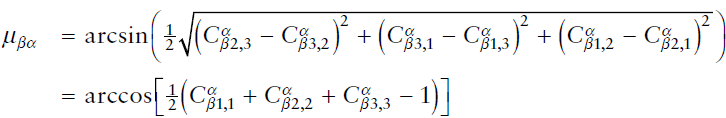
위 결과를 가지고 다음과 같이 나타내는 표기방식을 “쿼터니언”이라고 한다.

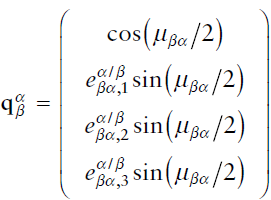
쿼터니언만 놓고 보면 회전에 대한 정보가 많이 압축 되어있어 물리적 해석을 위해 오일러각으로 변환하는데 시간이 소요된다. 그러나 DCM보다 더 차원이 줄었기 때문에 computation 상에서 이점이 있다.

1.4. Rotation vector

쿼터니언과 같은 4차원이 아니라 3차원으로 표현하는 방식도 있다. 이를 rotation vector라고 한다.

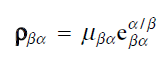
2. Frame 간 kinematics

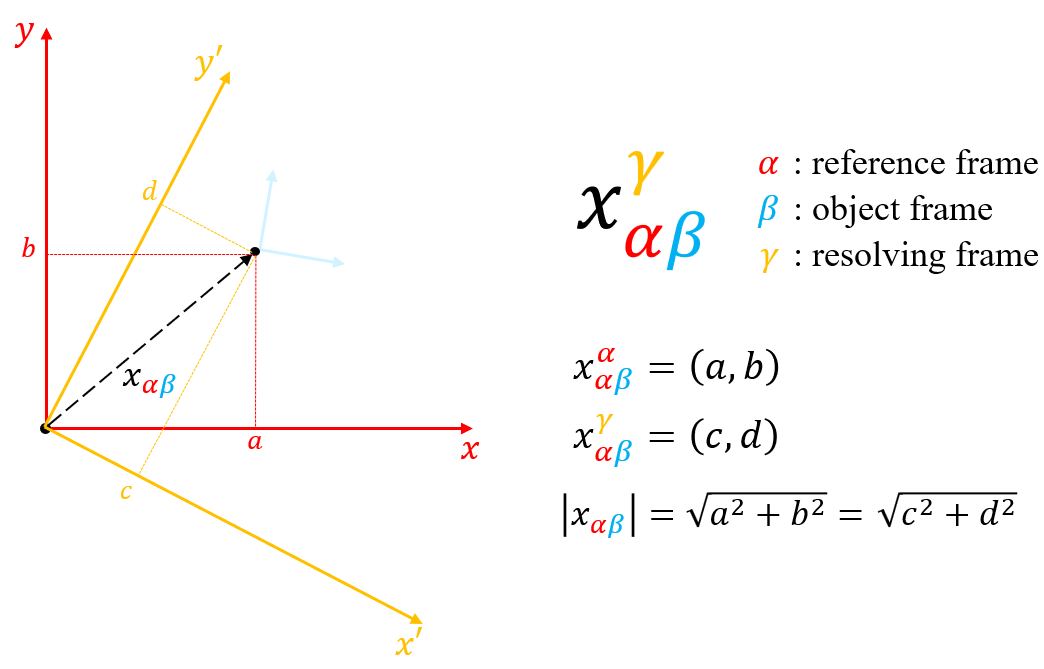
회전과 위치 벡터의 변환은 속도 및 가속도에 비해 단순한 편

2.1 Angular rate의 변환

[Basic 변환]

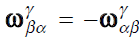
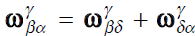
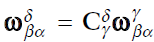
• 회전 행렬의 resolving frame 변환에 주의한다

  

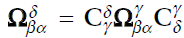
• 회전 행렬의 변화율

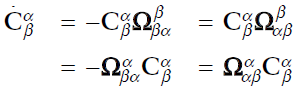
2.2 Cartesian position의 변환

[Basic 변환]

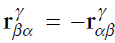
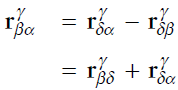
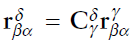
2.3. Velocity의 변환

[Basic 변환]

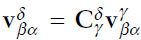
미분은 resolving frame과 reference frame이 같을 때만 가능하다.

Resolving frame과 reference frame이 다를 때 속도는 아래와 같이 유도된다.

\[\begin{aligned} \dot{r}_{\beta\alpha}^{\gamma}&=\frac{d}{dt}{(\textbf{C}_{\beta}^\gamma r_{\beta\alpha}^{\beta})}\\ &=\dot{\textbf{C}}_\beta^\gamma r_{\beta\alpha}^\beta+\textbf{C}_{\beta}^\gamma v_{\beta\alpha}^{\beta}\\ &=\dot{\textbf{C}}_\beta^\gamma r_{\beta\alpha}^\beta+v_{\beta\alpha}^{\gamma} \end{aligned}\]

Resolving frame과 reference frame간 자세변화율이 없다면 \(\dot{r}_{\beta\alpha}^\gamma = v_{\beta\alpha}^\gamma\) 이다.

벡터의 반전은 아래와 같이 유도된다.

\[\begin{aligned} \dot{r}_{\beta\alpha}^{\gamma}&=\frac{d}{dt}{(-\textbf{C}_{\alpha}^\gamma r_{\alpha\beta}^{\alpha})}\\ &=-\dot{\textbf{C}}_\alpha^\gamma r_{\alpha\beta}^\alpha-\textbf{C}_{\alpha}^\gamma v_{\alpha\beta}^{\alpha}\\ &=-\dot{\textbf{C}}_\alpha^\gamma r_{\alpha\beta}^\alpha-v_{\alpha\beta}^{\gamma} \end{aligned}\]

$\dot{r}_{\beta\alpha}^{\gamma}$에서 유도된 두 식의 결과는 같아야 하므로

\[\dot{\textbf{C}}_\beta^\gamma r_{\beta\alpha}^\beta+v_{\beta\alpha}^{\gamma}=-\dot{\textbf{C}}_\alpha^\gamma r_{\alpha\beta}^\alpha-v_{\alpha\beta}^{\gamma}\]

정리하면

\[\begin{aligned} v_{\beta\alpha}^{\gamma}&=-v_{\alpha\beta}^{\gamma}-\dot{\textbf{C}}_\alpha^\gamma r_{\alpha\beta}^\alpha- \dot{\textbf{C}}_\beta^\gamma r_{\beta\alpha}^\beta\\ &=-v_{\alpha\beta}^{\gamma}-\mathbf{\Omega}_{\gamma\alpha}^\gamma\textbf{C}_\alpha^\gamma r_{\alpha\beta}^\alpha- \mathbf{\Omega}_{\gamma\beta}^\gamma\textbf{C}_\beta^\gamma r_{\beta\alpha}^\beta\\ &=-v_{\alpha\beta}^{\gamma}-\mathbf{\Omega}_{\beta\alpha}^\gamma r_{\alpha\beta}^\gamma\\ &=-v_{\alpha\beta}^{\gamma}-\textbf{C}_\alpha^\gamma \mathbf{\Omega}_{\beta\alpha}^\alpha\textbf{C}_\gamma^\alpha r_{\alpha\beta}^\gamma\\ &=-v_{\alpha\beta}^{\gamma}-\textbf{C}_\alpha^\gamma \mathbf{\Omega}_{\beta\alpha}^\alpha\textbf{C}_\beta^\alpha \textbf{C}_\alpha^\beta \textbf{C}_\gamma^\alpha r_{\alpha\beta}^\gamma\\ &=-v_{\alpha\beta}^{\gamma}-\textbf{C}_\alpha^\gamma \dot{\textbf{C}}_\beta^\alpha r_{\alpha\beta}^\beta \end{aligned}\]

reference frame 과 object frame간 자세변화율이 없다면 $v_{\beta\alpha}^\gamma= -v_{\alpha\beta}^\gamma$ 이다.

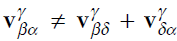
2.4 Acceleration의 변환

[Basic 변환]

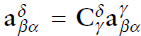
속도와 마찬가지로 미분은 resolving frame과 reference frame이 같을 때만 가능하다.

속도에서 유도한 것과 같은 방식으로 가속도는 다음과 같이 유도된다.

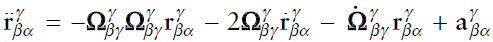
가속도 벡터의 반전, 합도 마찬가지로 일반적으로 성립하지 않는다.

3. Frame 별 관성항법 solution

어느 frame에서 표현하든 간에 관성항법 block diagram은 다음의 양상을 따른다.

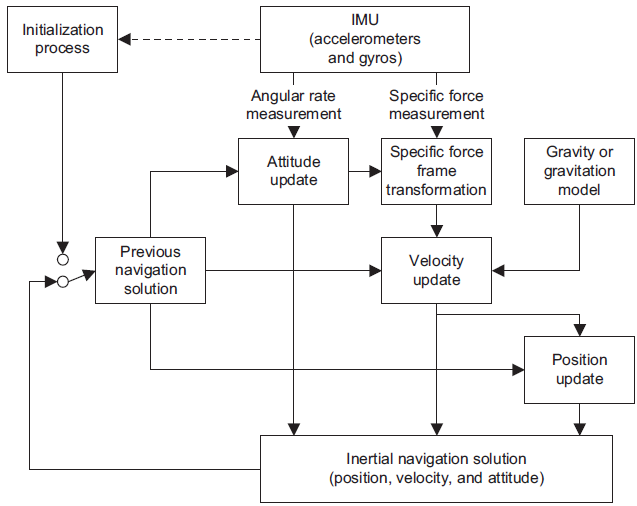
3.1 Inertial-Frame

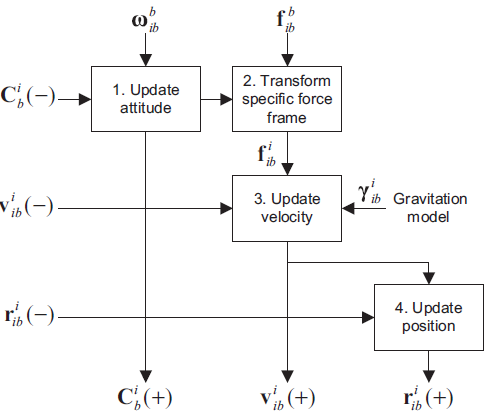
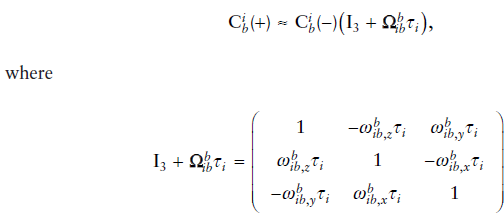
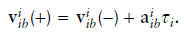
where

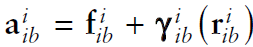
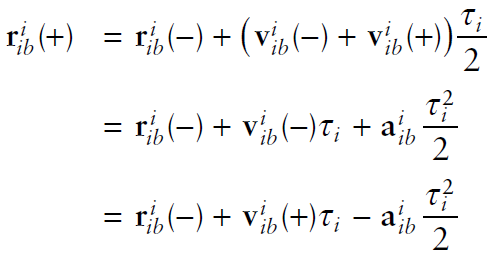
3.2 Earth-Frame

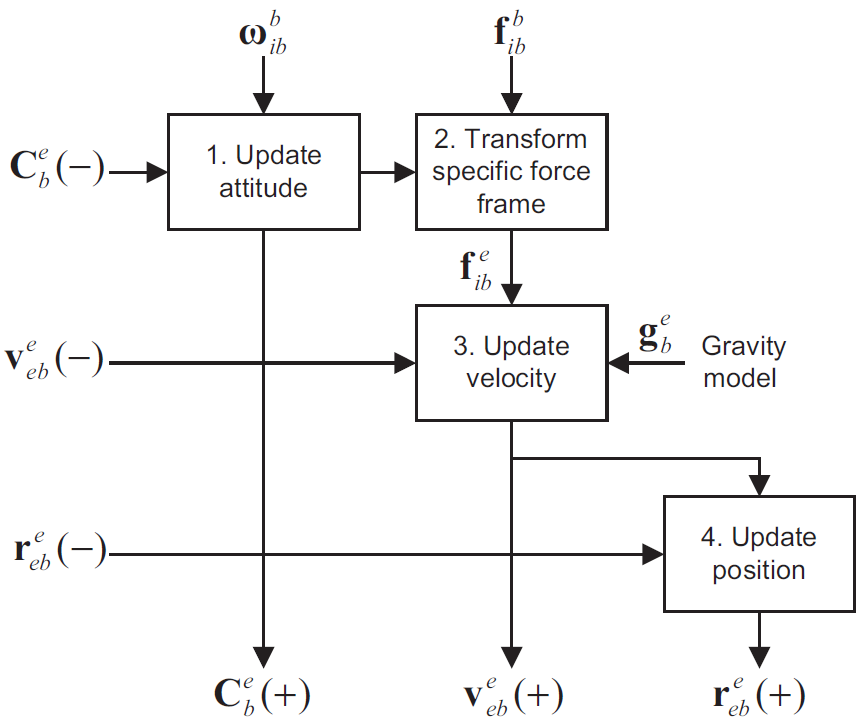
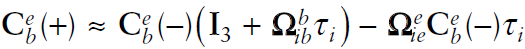
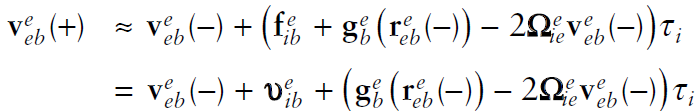
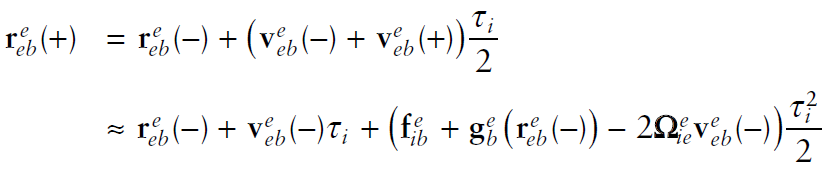
3.3 Local-Frame

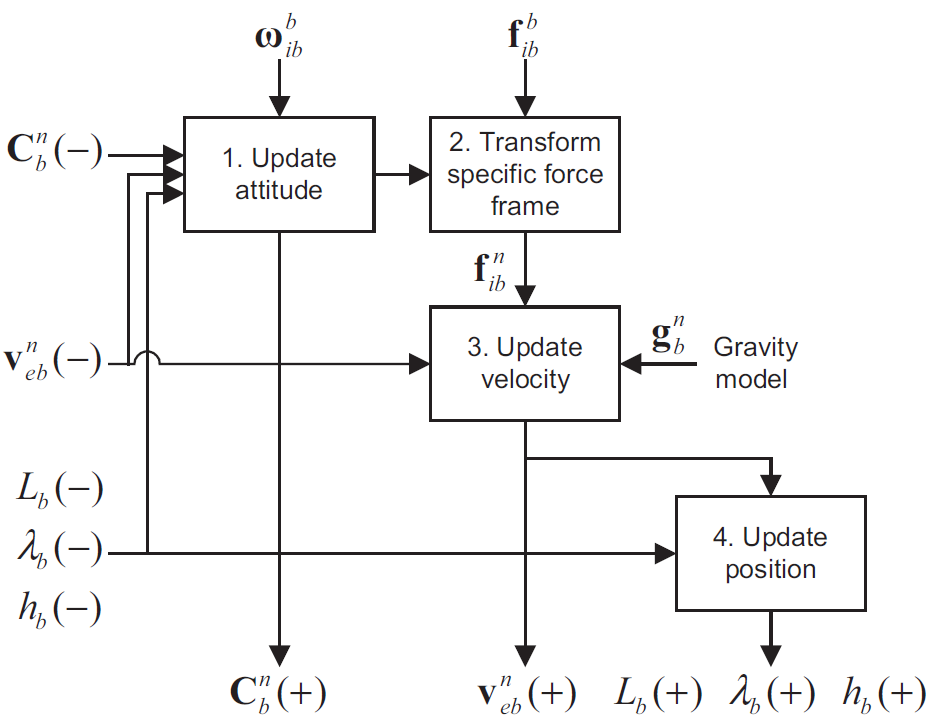
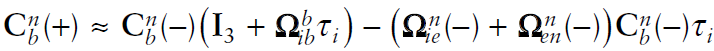
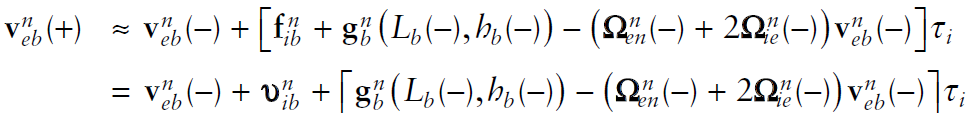
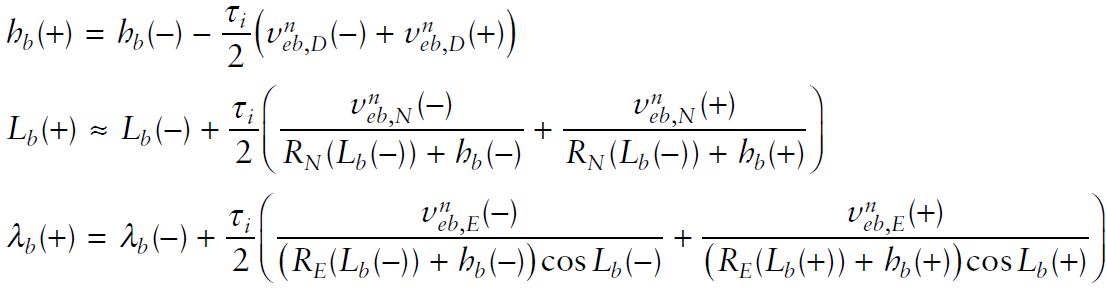
3.4 자세 갱신 Detail

[DCM 연산]

3.1~3.3에서 모두 $\dot{\textbf{C}}=\textbf{C}\mathbf{\Omega{}}$의 근사된 해를 사용해서 자세를 update 했다. $\dot{\textbf{C}}=\textbf{C}\mathbf{\Omega{}}$해의 정확도를 높이는 방식은 다음과 같다.

• $\dot{\textbf{C}}=\textbf{C}\mathbf{\Omega{}}$는 $\mathbf{C}$에 대한 미분 방정식으로, discrete version 해는 아래와 같이 나타낼 수 있다.
  • 여기서 $\Omega=[\omega_{nb}^b\times]$로, gyroscope의 값으로 구성된 skew symmatrix matrix

\[\mathbf{C}_{k+1}=\mathbf{C}_{k}\exp(\int_{t_k}^{t_{k+1}}\Omega dt)\]

• Sampling time epoch에 해당하는 $t_k$와 $t_{k+1}$사이에서 각속도 $\Omega$가 일정하다고 가정하면

  \[\mathbf{C}_{k+1}=\mathbf{C}_{k}\exp[\mathbf{\sigma} \times]\]
  • 여기서 $\sigma=\omega\Delta{t}$
  • 3.1~3.3의 결과는 모두 exp(matrix)의 1차 taylor 근사 결과이다.

• $[\mathbf{\sigma}\times]$가 skew symmatrix matrix임을 이용할 때 $\exp[\mathbf{\sigma}\times]$를 taylor expansion 하면

  

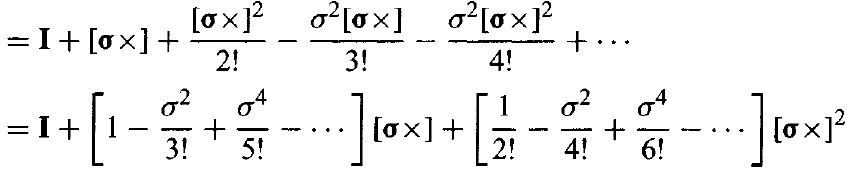
  • 이를 더 정리하면 아래와 같다.

    

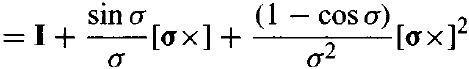
  • 연산량을 신경 안쓸거면 sin, cos 연산을 하면 되지만 sin, cos을 각각 second order 까지 근사한 결과만 써도 정확해진다.

[Quaternion 연산]

자세 계산을 쿼터니언으로 하면 DCM을 사용하는 것 보다 정확도가 4배로 올라간다[2]. 쿼터니언 기반 자세 갱신 과정은 다음과 같다.

• 쿼터니언의 미분은 아래와 같다고 알려져 있다. ([1] 참고)

  \[\dot{\mathbf{q}}=0.5\mathbf{q}\cdot\mathbf{p}\]
  • 여기서 $\mathbf{p}=[0,{w_{nb}^b}^T]$로, gyroscope로 만듦
  • 쿼터니언곱은 일반 벡터의 곱과 연산 내용이 다르다. ([1] 참고)

• 이를 행렬과 벡터의 곱으로 나타내면 아래와 같이 표현된다고 알려져 있다.

  \[\dot{\mathbf{q}}=0.5\mathbf{W}\mathbf{q}\]
  • where

  

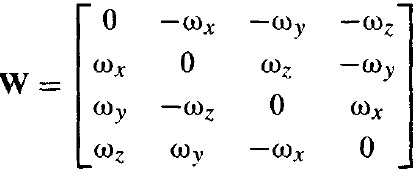
• 이는 위에서 풀었던 미분방정식과 같은 형태이다. discrete version 해는 아래와 같다.

  \[\mathbf{q}_{k+1}=\exp(0.5\mathbf{\Sigma})\mathbf{q}_k\]
  • 여기서 $\mathbf{\Sigma}$는

  

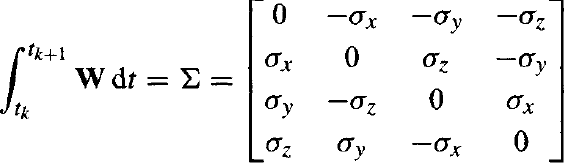
• Taylor expansion을 통해 정리하고 나면 다시 쿼터니언 곱의 형태로 나타낼 수 있다.

  \[\mathbf{q}_{k+1}=\mathbf{q}_{k}\cdot\mathbf{r}_{k}\]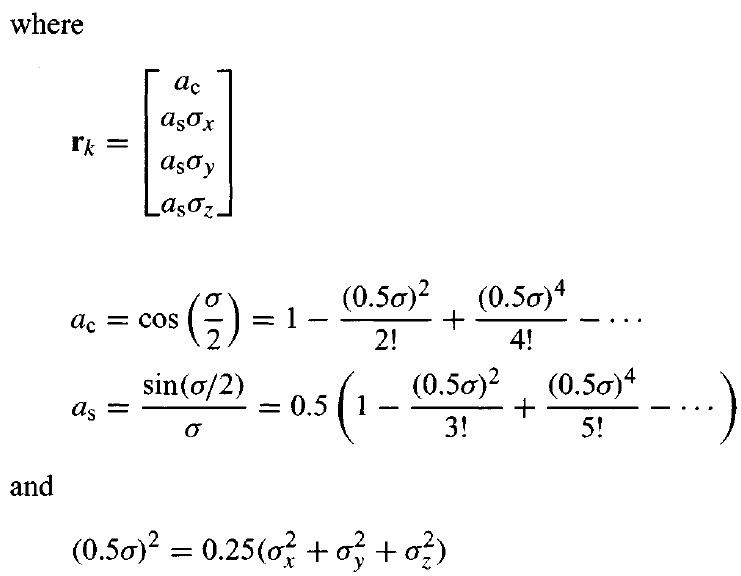

  

  • 연산량을 고려하여 sin과 cos을 적당히 각각 second order approximate로 근사
  • 계산된 쿼터니언을 다시 DCM으로 옮겨서 속도 및 위치 갱신
  • Quaternion u = [a b c d], v = [e f g h], 그리고 [b c d]를 벡터 r, [f g h]를 벡터 s라고 하면 quaternion 곱은 아래와 같다[1].
  \[\mathbf{u}\cdot\mathbf{v}=\mathbf{r}\times\mathbf{s}-\mathbf{r}\cdot\mathbf{s}+a\mathbf{s}+e\mathbf{r}+ae\]

아래의 coning 및 sculling 보정은 항체가 심한 진동을 겪을 때 사용한다. (IMU sampling rate와 진동에 의한 주파수가 맞먹을 때) Computational load가 달리는 예전에나 썼었지, 요새는 이 계산을 할 바에 imu sampling rate마다 자세 갱신을 한다.

Coning correction[2]

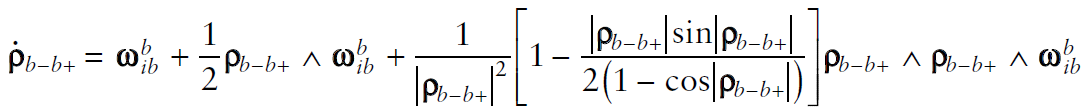
위 식에 대한 해는 아래와 같이 근사할 수 있다. (rotation vector에 대한 미분방정식)

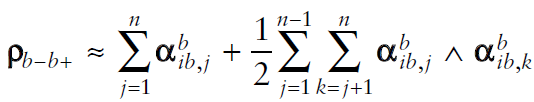
Sculling correction[2]

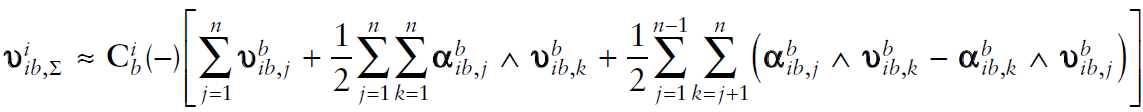
Appendix 1. 지표면 모델

물체의 위치를 원점이 지구 중심인 Cartesian 좌표계로 나타내는 것보다 위도, 경도, 고도를 이용한 방식이 더 직관적이다.

• 곡선의 지표면을 타원형으로 모델링해서 curvilinear position을 정의한다.

  

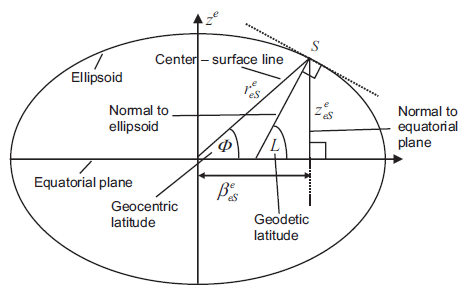
• 중력은 사실 지구 중심을 향하지 않는다. 이는 3.6에 기술한 원심력 때문이다. (appendix 3 참고) 실제 중력이 향하는 선과 equatorial plane이 교차하는 곳을 geodetic center라고 한다.
  • 지구를 타원형으로 모델링할 때 타원에 normal한 방향이 실제 중력의 방향이라고 가정한다.

• S에 위치한 local frame의 north-down($R_N$), east-down($R_E$) 방향으로 자른 타원의 곡률은 아래와 같이 유도된다.

  

  

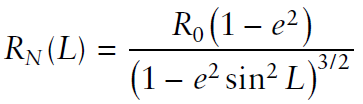
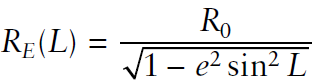
  • 여기서 e는 타원의 eccentricity이다. ($R_0$=equatorial radius, $R_p$=polar radius)

    

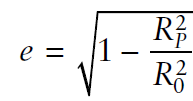
• S에 위치한 body frame의 위도, 경도, 고도 변화율은 아래와 같이 유도된다.

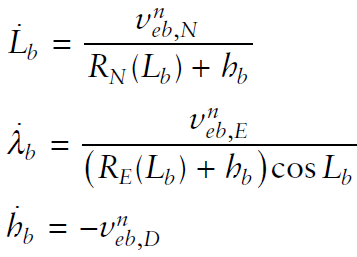
Appendix 2. 중력 모델

• IMU가 측정하는 값은 중력이 보상된 값이다. (책상위에 정지된 상태여도 중력 가속도 9.81 언저리 값이 찍힘)
  • 물체의 z축 방향 가속도를 계산할 때 : IMU 측정치 - 중력값(중력 모델을 따름)
• 따라서 정확한 중력 모델을 사용할수록 관성항법 성능이 향상된다

Appendix 3. Reference frame이 회전할 때 생기는 pseudo-acceleration

등속으로 회전하는 reference에 대해서 object frame에 가해지는 fictious 가속도는 다음과 같다.

• Centrifugal force (원심력)
  • 회전 중심에서 멀어지는 방향으로 작용
• Coriolis force
  • reference 기준 object 의 속도에 수직인 방향으로 작용 (속도가 0이면 없음)
  • 아래 동영상의 reference frame은 회전체, object frame은 공

  https://youtube.com/shorts/PFWdZHAhaho?si=JCWMhrfVP9SGOOBJ

  • 물론 reference frame이 회전체 밖에 서있는 선생님이라면 공은 직선운동을 하는 것 처럼 보일 것이다.

추가적으로 reference의 회전에 각가속도가 적용되는 경우 아래의 fictious 가속도가 추가된다.

• Euler force

Reference

[1] SAVAGE, RG.: ‘Strapdown analytics’, Strapdown Associates, Inc

[2] D. H. Titterton “Strapdown Inertial Navigation technology” 2nd ed

[3] P. D. Groves, “Principles of GNSS, Inertial, and multisensor integrated navigation systems” 2nd ed